题目内容

12．学校开设美术、舞蹈、计算机三门选修课，现有四名同学参与选课，且每人限选一门课程，那么不同的选课方法的种数是（　　）
A．12B．24C．64D．81

分析 四名同学参与选课，且每人限选一门课程，每人有4种选法，根据分步计数原理可得．

解答 解：四名同学参与选课，且每人限选一门课程，每人有4种选法，共有3×3×3×3=81种，
故选：D．

点评 本题主要考查排列、组合以及简单计数原理的应用，体现了分类讨论的数学思想，属于基础题．

练习册系列答案
相关题目
2．已知α的终边在第一象限，则角$\frac{α}{2}$的终边在（　　）
A．第一象限B．第二象限C．第一或第三象限D．第一或第四象限
3．命题p：?x∈R，2x＜3x；命题q：?x∈R，$\sqrt{x}=lo{g}_{\frac{1}{2}}x$，则下列命题中为真命题的是（　　）
A．p∧qB．￢p∧qC．p∧￢qD．￢p∧￢q
20．袋中有白球2个，红球3个，从中任取两个，则互斥且不对立的两个事件是（　　）
A．至少有一个白球；都是白球B．两个白球；至少有一个红球
C．红球、白球各一个；都是白球D．红球、白球各一个；至少有一个白球
7．若a+2bi=2-ai，其中a，b都是实数，i是虚数单位，则|a+bi|=$\sqrt{5}$．
17．设（2x-1）5=a0+a1（x-1）+a2（x-1）2+…+a5（x-1）5，则a0+a1+a2+…+a5的值为（　　）
A．1B．-1C．243D．-243
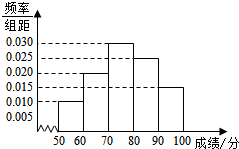4．对某次联考数学成绩（百分制）进行分析，如图为分析结果的频率分布直方图．根据标准，成绩分数在区间[50，60）上为不及格，在[60，70）上为一般，在[70，80）上为较好，在[80，90）上为良好，在[90，100]上为优秀．用频率估计概率，若从参考学生中随机抽取1人，则其成绩为优良（优秀或良好）的概率为（　　）
A．0.09B．0.20C．0.25D．0.40
1．已知双曲线$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1（a＞0，b＞0）的一条渐近线方程是y=x，它的一个焦点在抛物线y2=24x的准线上，则双曲线的方程为$\frac{{x}^{2}}{18}-\frac{{y}^{2}}{18}=1$．
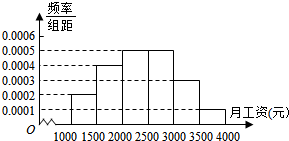6．进入2014年金秋，新入职的大学生陆续拿到了第一份薪水．某地调查机构就月薪情况调查了1000名新入职大学生，并根据所得数据画出样本的频率分布直方图（每个分组包括左端点，不包括右端点，如第一组表示月薪在[1000，1500）单位：元）．
（Ⅰ）求新入职大学生的月薪在[3000，4000）的频率，并根据频率分布直方图估计出样本数据的中位数；
（Ⅱ）为了分析新入职大学生的月薪与其性别的关系，必须按月薪再从这 1000人中按分层抽样方法抽出100人作进一步分析，已知月薪在[3500，4000）的被抽取出的人中恰有2位女性．若从月薪在[3500，4000）的被抽取出的人随机选出2人填写某项调查问卷，求这2人中至少有一位男性的概率．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网