题目内容
14.先后抛掷两枚均匀的骰子,若骰子朝上一面的点数依次为x,y(x,y∈{1,2,3,4,5,6}),则logx(2y-1)>1的概率是$\frac{19}{36}$.分析 本题是一个等可能事件的概率,试验发生包含的事件是6×6种结果,满足条件的事件需要先整理出关于x,y之间的关系,得到x<2y-1,根据条件列举出可能的情况,根据概率公式得到结果.
解答 解:由题意知,本题是一个等可能事件的概率,
试验发生包含的事件是6×6=36种结果,
∵logx(2y-1)>1,
∴x<2y-1,且x≠1,
∵x∈{1,2,3,4,5,6},y∈{1,2,3,4,5,6},
∴共有:(2,2),
(2,3),(3,3),(4,3),
(2,4),(3,4),(4,4,),(5,4),(6,4),
(2,5),(3,5),(4,5,),(5,5),(6,5),
(2,6),(3,6),(4,6,),(5,6),(6,6),共19种情况.
∴P=$\frac{19}{36}$,
故答案为:$\frac{19}{36}$
点评 本题考查等可能事件的概率,考查对数的运算,通过列举的方法得到需要的结果,本题是一个综合题,注意对于对数式的整理.

练习册系列答案
相关题目
20.袋中有白球2个,红球3个,从中任取两个,则互斥且不对立的两个事件是( )
| A. | 至少有一个白球;都是白球 | B. | 两个白球;至少有一个红球 | ||
| C. | 红球、白球各一个;都是白球 | D. | 红球、白球各一个;至少有一个白球 |
19.同时掷两个骰子,向上的点数不相同的概率为( )
| A. | $\frac{5}{6}$ | B. | $\frac{1}{6}$ | C. | $\frac{2}{3}$ | D. | $\frac{1}{3}$ |
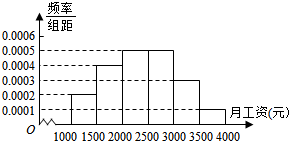 进入2014年金秋,新入职的大学生陆续拿到了第一份薪水.某地调查机构就月薪情况调查了1000名新入职大学生,并根据所得数据画出样本的频率分布直方图(每个分组包括左端点,不包括右端点,如第一组表示月薪在[1000,1500)单位:元).
进入2014年金秋,新入职的大学生陆续拿到了第一份薪水.某地调查机构就月薪情况调查了1000名新入职大学生,并根据所得数据画出样本的频率分布直方图(每个分组包括左端点,不包括右端点,如第一组表示月薪在[1000,1500)单位:元).