题目内容
如图,已知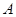 、
、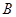 、
、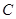 是长轴长为
是长轴长为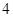 的椭圆上的三点,点
的椭圆上的三点,点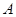 是长轴的一个顶点,
是长轴的一个顶点,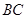 过椭圆中心
过椭圆中心 ,且
,且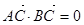 ,
,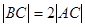 ,
,
(1)求椭圆的方程;
(2)如果椭圆上两点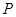 、
、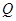 使
使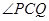 的平分线垂直
的平分线垂直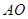 ,则是否存在实数
,则是否存在实数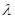 使
使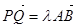 ?请说明理由。
?请说明理由。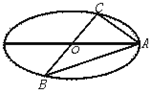
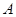 、
、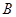 、
、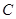 是长轴长为
是长轴长为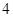 的椭圆上的三点,点
的椭圆上的三点,点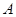 是长轴的一个顶点,
是长轴的一个顶点,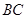 过椭圆中心
过椭圆中心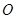 ,且
,且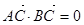 ,
,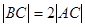 ,
,(1)求椭圆的方程;
(2)如果椭圆上两点
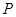 、
、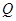 使
使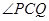 的平分线垂直
的平分线垂直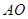 ,则是否存在实数
,则是否存在实数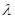 使
使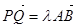 ?请说明理由。
?请说明理由。
(1)以O为原点,OA所在的直线为x轴建立如图所示的直角坐标系
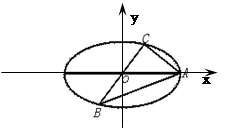
则A(2,0),设所求椭圆的方程为: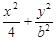 =1(0<b<2),
=1(0<b<2),
由椭圆的对称性知|OC|=|OB|,由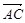 ·
·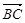 =0得AC⊥BC,
=0得AC⊥BC,
∵|BC|=2|AC|,∴|OC|=|AC|,
∴△AOC是等腰直角三角形,∴C的坐标为(1,1),∵C点在椭圆上
∴ =1,∴b2=
=1,∴b2=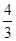 ,所求的椭圆方程为
,所求的椭圆方程为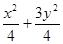 =1 ……………5分
=1 ……………5分
(2)由于∠PCQ的平分线垂直OA(即垂直于x轴),不妨设直线PC的斜率为k,则直线QC的斜率为-k,直线PC的方程为:y=k(x-1)+1,直线QC的方程为y=-k(x-1)+1,
由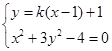 得:(1+3k2)x2-6k(k-1)x+3k2-6k-1=0(*) ……………8分
得:(1+3k2)x2-6k(k-1)x+3k2-6k-1=0(*) ……………8分
∵点C(1,1)在椭圆上,∴x=1是方程(*)的一个根,则其另一根为 ,设P(xP,yP),?Q(xQ,yQ),xP=
,设P(xP,yP),?Q(xQ,yQ),xP= , 同理xQ=
, 同理xQ= ,
,
kPQ=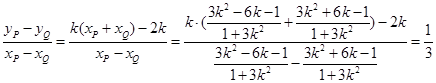 …10分
…10分
而由对称性知B(-1,-1),又A(2,0) ∴kAB=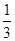
∴kPQ=kAB,∴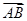 与
与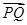 共线,且
共线,且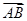 ≠0,即存在实数λ,使
≠0,即存在实数λ,使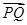 =λ
=λ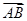 .
.

则A(2,0),设所求椭圆的方程为:
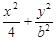 =1(0<b<2),
=1(0<b<2),由椭圆的对称性知|OC|=|OB|,由
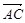 ·
·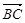 =0得AC⊥BC,
=0得AC⊥BC,∵|BC|=2|AC|,∴|OC|=|AC|,
∴△AOC是等腰直角三角形,∴C的坐标为(1,1),∵C点在椭圆上
∴
 =1,∴b2=
=1,∴b2=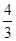 ,所求的椭圆方程为
,所求的椭圆方程为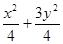 =1 ……………5分
=1 ……………5分 (2)由于∠PCQ的平分线垂直OA(即垂直于x轴),不妨设直线PC的斜率为k,则直线QC的斜率为-k,直线PC的方程为:y=k(x-1)+1,直线QC的方程为y=-k(x-1)+1,
由
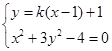 得:(1+3k2)x2-6k(k-1)x+3k2-6k-1=0(*) ……………8分
得:(1+3k2)x2-6k(k-1)x+3k2-6k-1=0(*) ……………8分∵点C(1,1)在椭圆上,∴x=1是方程(*)的一个根,则其另一根为
 ,设P(xP,yP),?Q(xQ,yQ),xP=
,设P(xP,yP),?Q(xQ,yQ),xP= , 同理xQ=
, 同理xQ= ,
, kPQ=
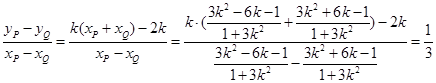 …10分
…10分而由对称性知B(-1,-1),又A(2,0) ∴kAB=
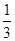
∴kPQ=kAB,∴
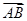 与
与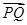 共线,且
共线,且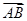 ≠0,即存在实数λ,使
≠0,即存在实数λ,使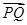 =λ
=λ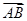 .
.(Ⅰ)根据椭圆的标准方程可知应以O为原点,OA所在的直线为x轴建立直角坐标系,然后由条件可知△ABC是直角三角形,进可确定△AOC是等腰直角三角形,这样易得C(1,1),代入椭圆标准方程问题可解.(2)涉及直线与椭圆的位置关系,然后两方程联立,利用韦达定理,解决交点坐标的问题,然后再借助向量共线的条件进行证明即可.

练习册系列答案
 优生乐园系列答案
优生乐园系列答案
相关题目
 的一个焦点是
的一个焦点是 ,那么实数
,那么实数 的值为( )
的值为( )



 轴上的椭圆
轴上的椭圆 的离心率为
的离心率为 ,且经过点
,且经过点 ,过点
,过点 的直线
的直线 与椭圆
与椭圆 .
. 的方程;
的方程; ?若存在,求出直线
?若存在,求出直线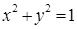 ,点O为坐标原点,一条直线:
,点O为坐标原点,一条直线: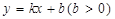 与圆O相切并与椭圆
与圆O相切并与椭圆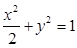 交于不同的两点A、B
交于不同的两点A、B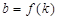 ,求
,求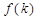 的表达式;
的表达式; 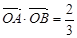 ,求直线的方程;
,求直线的方程;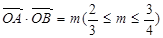 ,求三角形OAB面积的取值范围.
,求三角形OAB面积的取值范围. ,BM=
,BM= ,椭圆C以A,B为焦点且过点N.
,椭圆C以A,B为焦点且过点N.
 ,问是否存在不平行AB的直线L与椭圆C交于P,Q两点,且|PE|=|QE|,若存在,求出直线L与AB夹角的范围;若不存在,说明理由?
,问是否存在不平行AB的直线L与椭圆C交于P,Q两点,且|PE|=|QE|,若存在,求出直线L与AB夹角的范围;若不存在,说明理由?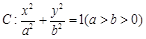 .
. ,
, 分别为椭圆
分别为椭圆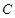 的左,右焦点,
的左,右焦点,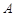
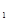 ,
, 分别为椭圆
分别为椭圆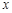 轴的直线与椭圆
轴的直线与椭圆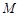
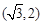 .
.
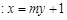 与椭圆
与椭圆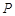 ,
,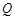 两点, 直线
两点, 直线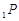 与
与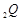 交于点
交于点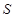 .当直线
.当直线
 且两两互相垂直的直线
且两两互相垂直的直线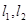 分别交椭圆
分别交椭圆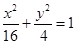 于
于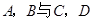 。(13分)
。(13分)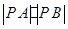 的最值
的最值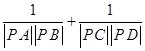 为定值
为定值 表示椭圆的充要条件是
表示椭圆的充要条件是 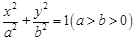 的右焦点为
的右焦点为 ,右准线为
,右准线为 ,若过点
,若过点 轴的弦的弦长等于点
轴的弦的弦长等于点