题目内容
已知椭圆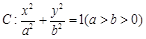 .
. ,
, 分别为椭圆
分别为椭圆 的左,右焦点,
的左,右焦点,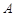
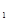 ,
,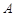
 分别为椭圆
分别为椭圆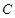 的左,右顶点.过右焦点
的左,右顶点.过右焦点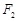 且垂直于
且垂直于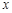 轴的直线与椭圆
轴的直线与椭圆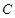 在第一象限的交点为
在第一象限的交点为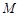
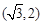 .
.
(1) 求椭圆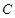 的标准方程;
的标准方程;
(2) 直线
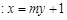 与椭圆
与椭圆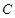 交于
交于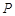 ,
,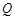 两点, 直线
两点, 直线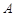
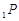 与
与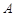
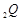 交于点
交于点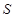 .当直线
.当直线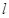 变化时, 点
变化时, 点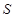 是否恒在一条定直线上?若是,求此定直线方程;若不是,请说明理由.
是否恒在一条定直线上?若是,求此定直线方程;若不是,请说明理由.
 .
.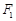 ,
,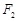 分别为椭圆
分别为椭圆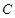 的左,右焦点,
的左,右焦点,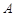
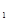 ,
,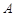
 分别为椭圆
分别为椭圆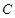 的左,右顶点.过右焦点
的左,右顶点.过右焦点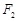 且垂直于
且垂直于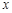 轴的直线与椭圆
轴的直线与椭圆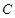 在第一象限的交点为
在第一象限的交点为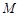
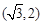 .
.(1) 求椭圆
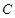 的标准方程;
的标准方程;(2) 直线
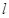
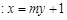 与椭圆
与椭圆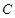 交于
交于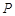 ,
,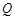 两点, 直线
两点, 直线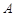
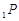 与
与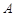
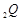 交于点
交于点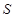 .当直线
.当直线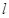 变化时, 点
变化时, 点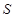 是否恒在一条定直线上?若是,求此定直线方程;若不是,请说明理由.
是否恒在一条定直线上?若是,求此定直线方程;若不是,请说明理由.
(1)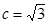 ,
, 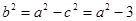 . 点
. 点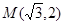 在椭圆上,
在椭圆上,
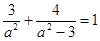 ,
, 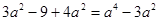
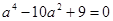
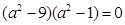
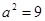 或
或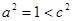 (舍去).
(舍去). 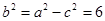 .
.
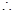 椭圆
椭圆 的方程为
的方程为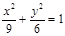 . ………4分
. ………4分
(2)当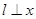 轴时,
轴时,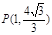 ,
,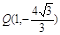 , 又
, 又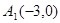 ,
, 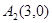
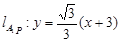 ,
, 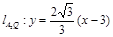 , 联立解得
, 联立解得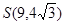 .
.
当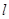 过椭圆的上顶点时,
过椭圆的上顶点时, 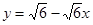 ,
,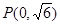 ,
, 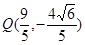
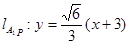 ,
, 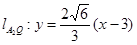 ,联立解得
,联立解得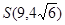 .
.
若定直线存在,则方程应是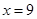 . ………8分
. ………8分
下面给予证明.
把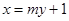 代入椭圆方程,整理得,
代入椭圆方程,整理得,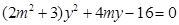
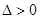 成立, 记
成立, 记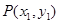 ,
, 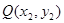 ,则
,则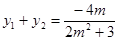 ,
, 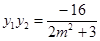 .
.
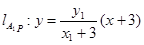 ,
, 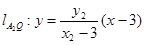
当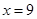 时,纵坐标
时,纵坐标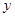 应相等,
应相等, 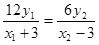 , 须
, 须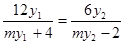
须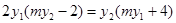 , 须
, 须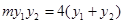
而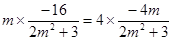 成立.
成立.
综上,定直线方程为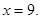
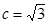 ,
, 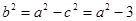 . 点
. 点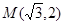 在椭圆上,
在椭圆上,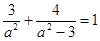 ,
, 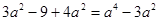
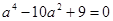
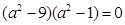
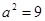 或
或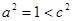 (舍去).
(舍去). 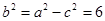 .
.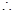 椭圆
椭圆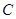 的方程为
的方程为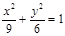 . ………4分
. ………4分(2)当
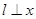 轴时,
轴时,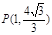 ,
,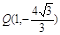 , 又
, 又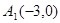 ,
, 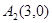
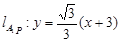 ,
, 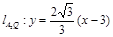 , 联立解得
, 联立解得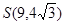 .
.当
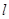 过椭圆的上顶点时,
过椭圆的上顶点时, 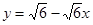 ,
,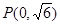 ,
, 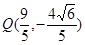
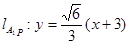 ,
, 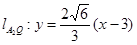 ,联立解得
,联立解得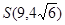 .
. 若定直线存在,则方程应是
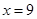 . ………8分
. ………8分 下面给予证明.
把
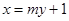 代入椭圆方程,整理得,
代入椭圆方程,整理得,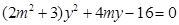
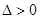 成立, 记
成立, 记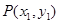 ,
, 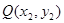 ,则
,则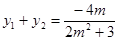 ,
, 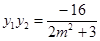 .
.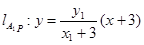 ,
, 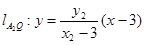
当
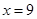 时,纵坐标
时,纵坐标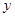 应相等,
应相等, 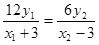 , 须
, 须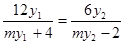
须
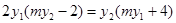 , 须
, 须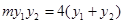
而
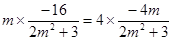 成立.
成立.综上,定直线方程为
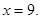
(1)根据条件易求c,然后根据点M在椭圆上建立方程即可求解。
(2)本题是探索性问题,应先假设存在,然后要对直线出现的各种情况讨论,分类解决。
(2)本题是探索性问题,应先假设存在,然后要对直线出现的各种情况讨论,分类解决。

练习册系列答案
相关题目
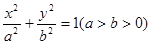 的右焦点为
的右焦点为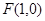 ,
,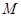 为椭圆的上顶点,
为椭圆的上顶点,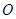 为坐标原点,且△
为坐标原点,且△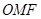 是等腰直角三角形.
是等腰直角三角形.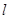 交椭圆于
交椭圆于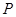 ,
,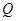 两点, 且使点
两点, 且使点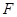 为△
为△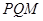 的垂心(垂心:三角形三边高线的交点)?若存在,求出直线
的垂心(垂心:三角形三边高线的交点)?若存在,求出直线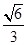 的椭圆
的椭圆
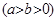 经过点
经过点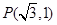 .
. 的方程;
的方程;  且不与
且不与 轴垂直的直线
轴垂直的直线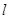 交椭圆
交椭圆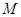 、
、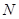 两点,若
两点,若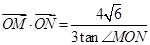 (
(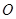 为坐标原点),求直线
为坐标原点),求直线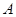 、
、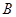 、
、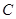 是长轴长为
是长轴长为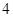 的椭圆上的三点,点
的椭圆上的三点,点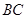 过椭圆中心
过椭圆中心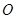 ,且
,且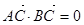 ,
,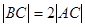 ,
,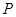 、
、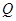 使
使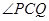 的平分线垂直
的平分线垂直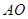 ,则是否存在实数
,则是否存在实数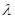 使
使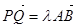 ?请说明理由。
?请说明理由。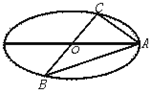
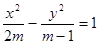 表示焦点在y轴上的椭圆;命题q:双曲线
表示焦点在y轴上的椭圆;命题q:双曲线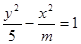 的离心率
的离心率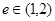 ,若p、q有且只有一个为真,求m的取值范围。
,若p、q有且只有一个为真,求m的取值范围。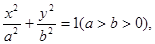 它的一个焦点与抛物线
它的一个焦点与抛物线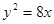 的焦点重合,离心率
的焦点重合,离心率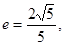 过椭圆的右焦点F作与坐标轴不垂直的直线
过椭圆的右焦点F作与坐标轴不垂直的直线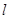 交椭圆于A、B两点.(Ⅰ)求椭圆的标准方程;
交椭圆于A、B两点.(Ⅰ)求椭圆的标准方程;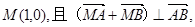 求直线
求直线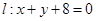 ,圆O:
,圆O: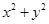 =36(O为坐标原点),椭圆C:
=36(O为坐标原点),椭圆C: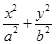 =1(a>b>0)的离心率为e=
=1(a>b>0)的离心率为e=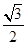 ,直线l被圆O截得的弦长与椭圆的长轴长相等。
,直线l被圆O截得的弦长与椭圆的长轴长相等。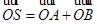 (O是坐标原点),是否存在这样的直线l,使四边形为ASB的对角线长相等?若存在 ,求出直线l的方程,若不存在,说明理由。
(O是坐标原点),是否存在这样的直线l,使四边形为ASB的对角线长相等?若存在 ,求出直线l的方程,若不存在,说明理由。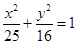 上任意一点,
上任意一点,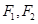 为左、右焦点,
为左、右焦点, 如图所示.
如图所示.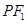 的中点为
的中点为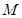 ,求证:
,求证: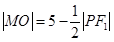
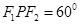 ,求|PF1|·|PF2|之值;
,求|PF1|·|PF2|之值;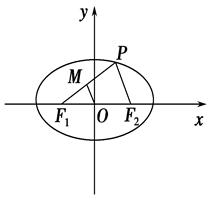
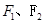 是椭圆
是椭圆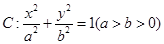 的两个焦点,P为椭圆
的两个焦点,P为椭圆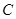 上的一点,且
上的一点,且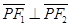 .若
.若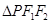 的面积为9,则
的面积为9,则 .
.