题目内容
已知数列{an}的通项公式为an=n2-n-30.
(1)求数列的前三项,60是此数列的第几项?
(2)n为何值时,an=0,an>0,an<0?
(3)该数列前n项和Sn是否存在最值?说明理由.
(1)求数列的前三项,60是此数列的第几项?
(2)n为何值时,an=0,an>0,an<0?
(3)该数列前n项和Sn是否存在最值?说明理由.
(1)第10项 (2)0<n<6(n∈N*) (3)不存在,见解析
解:(1)由an=n2-n-30,得
a1=1-1-30=-30,
a2=22-2-30=-28,
a3=32-3-30=-24.
设an=60,则60=n2-n-30.
解之得n=10或n=-9(舍去).
∴60是此数列的第10项.
(2)令an=n2-n-30=0,
解得n=6或n=-5(舍去),∴a6=0.
令n2-n-30>0,
解得n>6或n<-5(舍去).
∴当n>6(n∈N*)时,an>0.
令n2-n-30<0,解得0<n<6,
∴当0<n<6(n∈N*)时,an<0.
(3)Sn存在最小值,不存在最大值.
由an=n2-n-30=(n-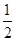 )2-30
)2-30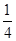 ,(n∈N*)
,(n∈N*)
知{an}是递增数列,且
a1<a2<…<a5<a6=0<a7<a8<a9<…,
故Sn存在最小值S5=S6,不存在Sn的最大值.
a1=1-1-30=-30,
a2=22-2-30=-28,
a3=32-3-30=-24.
设an=60,则60=n2-n-30.
解之得n=10或n=-9(舍去).
∴60是此数列的第10项.
(2)令an=n2-n-30=0,
解得n=6或n=-5(舍去),∴a6=0.
令n2-n-30>0,
解得n>6或n<-5(舍去).
∴当n>6(n∈N*)时,an>0.
令n2-n-30<0,解得0<n<6,
∴当0<n<6(n∈N*)时,an<0.
(3)Sn存在最小值,不存在最大值.
由an=n2-n-30=(n-
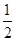 )2-30
)2-30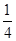 ,(n∈N*)
,(n∈N*)知{an}是递增数列,且
a1<a2<…<a5<a6=0<a7<a8<a9<…,
故Sn存在最小值S5=S6,不存在Sn的最大值.

练习册系列答案
 高中必刷题系列答案
高中必刷题系列答案
相关题目
 的首项
的首项 ,
, 是
是 项和,且
项和,且
 .
. ,求数列
,求数列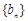 的通项公式;
的通项公式; ,证明:
,证明: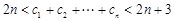 ,
, .
. <-1,且它们的前n项和Sn有最大值,则使Sn>0的n的最大值为________.
<-1,且它们的前n项和Sn有最大值,则使Sn>0的n的最大值为________.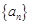 是等比数列, 且
是等比数列, 且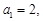
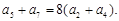 数列
数列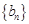 满足:对任意正整数
满足:对任意正整数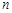 ,有
,有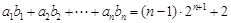 .
. 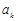 与
与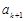 之间插入
之间插入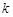 个
个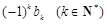 后,得到一个新的数列
后,得到一个新的数列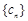 . 求数列
. 求数列 满足
满足 ,
, ,且
,且 ,则
,则 .
.