题目内容
已知数列 的首项
的首项 ,
, 是
是 的前
的前 项和,且
项和,且
 .
.
(1)若记 ,求数列
,求数列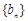 的通项公式;
的通项公式;
(2)记 ,证明:
,证明: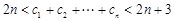 ,
, .
.
 的首项
的首项 ,
, 是
是 的前
的前 项和,且
项和,且
 .
.(1)若记
 ,求数列
,求数列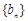 的通项公式;
的通项公式;(2)记
 ,证明:
,证明: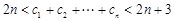 ,
, .
.(1) 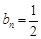 ;(2)详见解析.
;(2)详见解析.
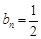 ;(2)详见解析.
;(2)详见解析.试题分析:(1)由
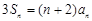 ,得:
,得: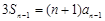
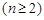 ,两式相加,得:
,两式相加,得: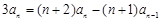 ,
,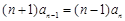
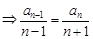 ,即
,即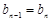 ,所以
,所以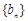 是常数列.又
是常数列.又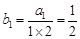 ,即可求出结果;(2)由(1)得
,即可求出结果;(2)由(1)得 ,进而可求
,进而可求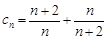 ,又
,又 ,所以
,所以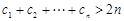 ;又由于
;又由于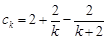 ,利于裂项相消法可求得
,利于裂项相消法可求得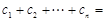
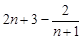
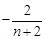 ,显然可证右边成立.
,显然可证右边成立.(1)由
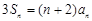 ,得:
,得: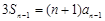
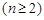 ,
,两式相加,得:
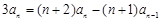 ,
,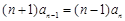
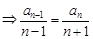
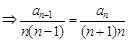 ,即
,即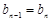 ,所以
,所以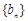 是常数列.
是常数列.又
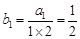 ,所以
,所以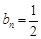 . .5分
. .5分(2)由(1)得
 ,从而
,从而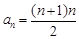 ,
,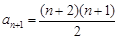 ,
, ,
,故
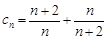 . .7分
. .7分由
 ,所以
,所以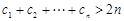 . 9分
. 9分又
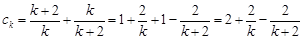 ,
,所以
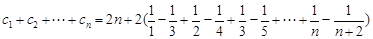
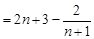
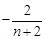
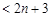 . .12分
. .12分(注:
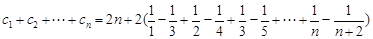
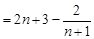
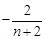 ,因为
,因为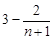
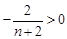 ,所以
,所以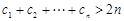 ).
).
练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
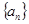 和
和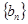 满足
满足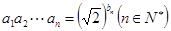 .若
.若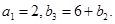
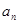 与
与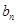 ;
;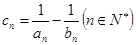 。记数列
。记数列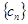 的前
的前 项和为
项和为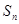 .
.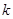 ,使得对任意
,使得对任意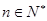 ,均有
,均有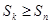 .
.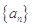 的首项
的首项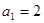 ,且对任意
,且对任意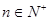 都有
都有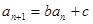 (其中
(其中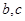 为常数).
为常数).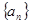 为等差数列,且
为等差数列,且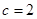 ,求
,求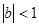 ,从数列
,从数列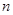 项和
项和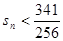 成立的
成立的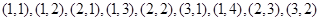 ,
,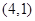 , ,则第60个数对是 .
, ,则第60个数对是 .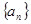 的各项均为正数,且
的各项均为正数,且
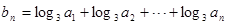 ,求数列
,求数列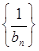 的前n项和
的前n项和 ;
;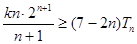 恒成立的实数
恒成立的实数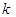 的取值范围.
的取值范围.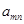 表示位于从上到下第
表示位于从上到下第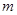 行,从左到右
行,从左到右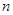 列的数,比如
列的数,比如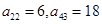 ,若
,若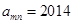 ,则有( )
,则有( )


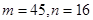

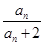 (n∈N*).若bn+1=(n-λ)(
(n∈N*).若bn+1=(n-λ)(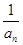 +1)(n∈N*),b1=-λ,且数列{bn}是单调递增数列,则实数λ的取值范围为( )
+1)(n∈N*),b1=-λ,且数列{bn}是单调递增数列,则实数λ的取值范围为( ) 中,若
中,若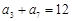 ,
,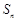 是
是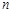 项和,则
项和,则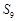 的值为
的值为