题目内容
【题目】某县相邻两镇在一平面直角坐标系下的坐标为A(1,2)、B(4,0),一条河所在直线方程为l:x+2y-10=0,若在河边l上建一座供水站P使之到A、B两镇的管道最省,问供水站P应建在什么地方?此时|PA|+|PB|为多少?
【答案】供水站应建在点![]() 处;
处; ![]()
【解析】试题分析:根据两点间的距离公式以及点的对称性,建立方程组的关系,进行求解即可.
试题解析:
如图所示,过A作直线l的对称点A′,连接A′B交l于P,因为若P′(异于P)在直线l上,则|AP′|+|BP′|=|A′P′|+|BP′|>|A′B|.
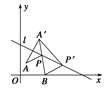
因此,供水站只能在点P处,才能取得最小值.
设A′(a,b),则AA′的中点在l上,且AA′⊥l,
即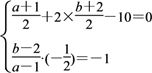 ,解得
,解得![]() ,即A′(3,6).
,即A′(3,6).
所以直线A′B的方程为6x+y-24=0.
解方程组![]() ,得
,得![]() .
.
所以P点的坐标为(![]() ,
,![]() ).
).
故供水站应建在点P(![]() ,
,![]() )处,
)处,
此时|PA|+|PB|=|A′B|=![]() =
=![]() .
.

练习册系列答案
相关题目