Question

【题目】如图，四棱锥S﹣ABCD中，AB∥CD，BC⊥CD，侧面SAB为等边三角形．AB=BC=2，CD=SD=1．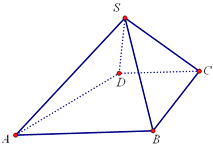
（1）证明：SD⊥平面SAB
（2）求AB与平面SBC所成角的正弦值．

Answer 1

【答案】
（1）证明：取AB中点E，连结DE，则四边形BCDE为矩形，DE=CB=2．

连结SE，则

又SD=1，故ED2=SE2+SD2

所以∠DSE为直角，

所以SD⊥SE，

由AB⊥DE，AB⊥SE，DE∩SE=E，得AB⊥平面SDE，所以AB⊥SD．

因为AB∩SE=E，

所以SD⊥平面SAB

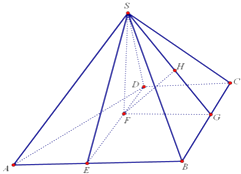
（2）解：由AB⊥平面SDE知，平面ABCD⊥平面SDE．

作SF⊥DE，垂足为F，则SF⊥平面ABCD，

作FG⊥BC，垂足为G，则FG=DC=1．

连结SG，则SG⊥BC

又FG⊥BC，SG∩FG=G，

故BC⊥平面SFG，平面SBC⊥平面SFG，

作FH⊥SG，H为垂足，则FH⊥平面SBC，

即F到平面SBC的距离为 ．

由于ED∥BC，所以ED∥平面SBC，E到平面SBC的距离d也为 ．

设AB与平面SBC所成的角为α，则 ．

【解析】（1）取AB中点E，连结DE，证明SD⊥平面SAB，只需证明SD⊥SE，AB⊥SD；（2）求出F到平面SBC的距离，由于ED∥BC，所以ED∥平面SBC，可得E到平面SBC的距离，从而可求AB与平面SBC所成角的正弦值．
【考点精析】掌握直线与平面垂直的判定和空间角的异面直线所成的角是解答本题的根本，需要知道一条直线与一个平面内的两条相交直线都垂直，则该直线与此平面垂直；注意点：a)定理中的“两条相交直线”这一条件不可忽视；b)定理体现了“直线与平面垂直”与“直线与直线垂直”互相转化的数学思想；已知为两异面直线，A，C与B，D分别是上的任意两点，所成的角为，则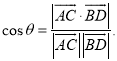．