Question

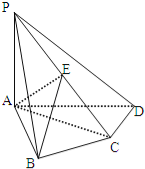
【题目】如图，四棱锥P﹣ABCD中，PA⊥底面ABCD，AB⊥AD，AC⊥CD，∠ABC=60°，PA=AB=BC，

E是PC的中点．求证：

（Ⅰ）CD⊥AE；

（Ⅱ）PD⊥平面ABE．

Answer 1

【答案】见解析

【解析】试题分析：（Ⅰ）先证明CD⊥平面PAC，然后证明CD⊥AE；

（Ⅱ）要证PD⊥平面ABE，只需证明PD垂直平面ABE内的两条相交直线AE与AB即可．

证明：（Ⅰ）∵PA⊥底面ABCD，∴PA⊥CD，又AC⊥CD，PA∩AC=A，

故CD⊥平面PAC．

又AE平面PAC，∴CD⊥AE．

（Ⅱ）由题意：AB⊥AD，

∴AB⊥平面PAD，从而AB⊥PD．

又AB=BC，且∠ABC=60°，

∴AC=AB，从而AC=PA．

又E为PC之中点，∴AE⊥PC．

由（Ⅰ）知：AE⊥CD，∴AE⊥平面PCD，从而AE⊥PD．

又AB∩AE=A，

故PD⊥平面ABE．