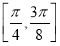题目内容
12．
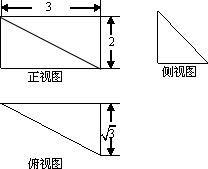某多面体的三视图如图所示，则该多面体最长的棱长为4；外接球的体积为$\frac{32π}{3}$．
分析 判断直观图的形状，利用三视图求解棱长与几何体的外接球的体积即可．
解答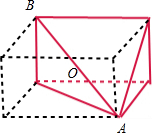 
解：由题意可知：几何体的直观图如图：几何体是四棱锥，是长方体的一部分，最长边为AB，AB=$\sqrt{{3}^{2}+{2}^{2}+{（\sqrt{3}）}^{2}}$=4，
四棱锥的外接球就是长方体的外接球，半径为：$\frac{AB}{2}=2$，外接球的体积为：$\frac{4π}{3}×{2}^{3}$=$\frac{32π}{3}$．
故答案为：4；$\frac{32π}{3}$．
点评 本题考查三视图与几何体的关系，判断三视图的形状是解题的关键，考查计算能力．
练习册系列答案
相关题目
5．设m，n是两条不同的直线，α，β是两个不同的平面，则（ ）
| A． | 若m∥α，m∥β，则α∥β | B． | 若m∥α，m∥n，则n∥α | C． | 若m⊥α，m∥β，则α⊥β | D． | 若m∥α，n?α，则m∥n |
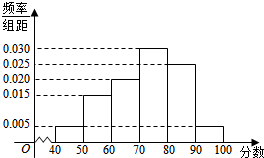某校对参加高校自主招生测试的学生进行模拟训练，从中抽出N名学生，其数学成绩的频率分布直方图如图所示．已知成绩在区间[90，100]内的学生人数为2人．
Rt△ABC中，∠C=90°，CD⊥AB，AD为圆O的直径，圆O与AC交于E，求证：$\frac{AE}{CE}$=$\frac{A{C}^{2}}{B{C}^{2}}$．
17．已知函数f（x）=$\frac{1}{x+2}$-k|x|（{k∈R}）有三个不同的零点，则实数k的取值范围是（ ）
| A． | （0，1） | B． | （0，2） | C． | （1，+∞） | D． | （2，+∞） |
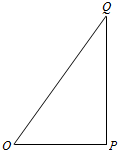如图，O，P，Q三地有直道相通，OP=3千米，PQ=4千米，OQ=5千米，现甲、乙两警员同时从O地出发匀速前往Q地，经过t小时，他们之间的距离为f（t）（单位：千米）．甲的路线是OQ，速度为5千米/小时，乙的路线是OPQ，速度为8千米/小时，乙到达Q地后在原地等待．设t=t1时乙到达P地，t=t2时乙到达Q地．
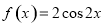的图象向右平移
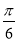个单位后得到函数
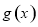的图象．若函数
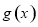在区间
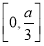和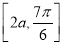
上均单调递增，则实数
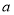的取值范围是（ ）
B．
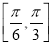D．