题目内容
4.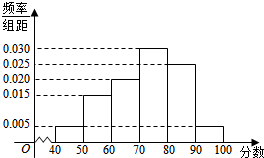 某校对参加高校自主招生测试的学生进行模拟训练,从中抽出N名学生,其数学成绩的频率分布直方图如图所示.已知成绩在区间[90,100]内的学生人数为2人.
某校对参加高校自主招生测试的学生进行模拟训练,从中抽出N名学生,其数学成绩的频率分布直方图如图所示.已知成绩在区间[90,100]内的学生人数为2人.(1)求N的值并估计这次测试数学成绩的平均分和众数;
(2)学校从成绩在[70,100]的三组学生中用分层抽样的方法抽取12名学生进行复试,若成绩在[80,90)这一小组中被抽中的学生实力相当,且能通过复试的概率均为$\frac{1}{2}$,设成绩在[80,90)这一小组中被抽中的学生中能通过复试的人数为ξ,求ξ的分布列和数学期望.
分析 (1)求出成绩在区间[90,100]内的频率为0.005×10=0.05,即可求N的值并估计这次测试数学成绩的平均分和众数;
(2)确定从这一小组中抽出的人数,依题意知$ξ~B(5,\frac{1}{2})$,求出相应的概率,即可求ξ的分布列和数学期望.
解答 解:(1)由频率分布直方图可知,成绩在区间[90,100]内的频率为0.005×10=0.05,所以$N=\frac{2}{0.05}=40$,利用中值估算抽样学生的平均分:45×0.05+55×0.15+65×0.2+75×0.3+85×0.25+95×0.05=72.
所以,估计这次考试的平均分是7(2分).
由频率分布直方图可知,成绩分布在[70,80]间的频率最大,所以众数的估计值为区间[70,80]的中点值7(5分)…(6分)
(注:这里的众数、平均值为估计量,若遗漏估计或大约等词语扣一分)
(2)由(1)知,成绩在[70,100]内的学生共有40×(0.3+0.25+0.05)=24人,成绩在[80,90)这一小组的人数有40×0.025=10人.所以从这一小组中抽出的人数为$\frac{12}{24}×10=5$人,
依题意知$ξ~B(5,\frac{1}{2})$,$P(x=k)=C_5^k{(\frac{1}{2})^k}•{(\frac{1}{2})^{5-k}}=C_5^k{(\frac{1}{2})^5}$,$P(ξ=0)=C_5^0{(\frac{1}{2})^5}=\frac{1}{32}$,$P(ξ=1)=C_5^1{(\frac{1}{2})^5}=\frac{5}{32}$,$P(ξ=2)=C_5^2{(\frac{1}{2})^5}=\frac{10}{32}$,$P(ξ=3)=C_5^3{(\frac{1}{2})^5}=\frac{10}{32}$,$P(ξ=4)=C_5^4{(\frac{1}{2})^5}=\frac{5}{32}$,$P(ξ=5)=C_5^5{(\frac{1}{2})^5}=\frac{1}{32}$,
所以ξ的分布列为:
| ξ | 0 | 1 | 2 | 3 | 4 | 5 |
| P | $\frac{1}{32}$ | $\frac{5}{32}$ | $\frac{10}{32}$ | $\frac{10}{32}$ | $\frac{5}{32}$ | $\frac{1}{32}$ |
点评 本题考查概率的求法,考查离散型随机变量的分布列和数学期望的求法,解题时要认真审题,注意频率分布直方图的合理运用.

 夺冠训练单元期末冲刺100分系列答案
夺冠训练单元期末冲刺100分系列答案 新思维小冠军100分作业本系列答案
新思维小冠军100分作业本系列答案 名师指导一卷通系列答案
名师指导一卷通系列答案 在四棱柱ABCD-A1B1C1D1中,AA1⊥平面A1B1C1D1,底面A1B1C1D1是边长为a的正方形,侧棱AA1的长为b,E为侧棱BB1上的动点(包括端点),则( )
在四棱柱ABCD-A1B1C1D1中,AA1⊥平面A1B1C1D1,底面A1B1C1D1是边长为a的正方形,侧棱AA1的长为b,E为侧棱BB1上的动点(包括端点),则( )| A. | 对任意的a,b,存在点E,使得B1D⊥EC1 | |
| B. | 当且仅当a=b时,存在点E,使得B1D⊥EC1 | |
| C. | 当且仅当a≤b时,存在点E,使得B1D⊥EC1 | |
| D. | 当且仅当a≥b时,存在点E,使得B1D⊥EC1 |
| A. | S2012=-2012,a2012>a7 | B. | S2012=2012,a2012>a7 | ||
| C. | S2012=-2012,a2012<a7 | D. | S2012=2012,a2012<a7 |
 如图,在三棱锥P-ABC中,△ABC是边长为2的正三角形,∠PCA=90°,E,H分别为AP,AC的中点,AP=4,BE=$\sqrt{3}$.
如图,在三棱锥P-ABC中,△ABC是边长为2的正三角形,∠PCA=90°,E,H分别为AP,AC的中点,AP=4,BE=$\sqrt{3}$. 如图:⊙O的直径AB的延长线于弦CD的延长线相交于点P,E为⊙O上一点,$\widehat{AE}$=$\widehat{AC}$,DE交AB于点F.
如图:⊙O的直径AB的延长线于弦CD的延长线相交于点P,E为⊙O上一点,$\widehat{AE}$=$\widehat{AC}$,DE交AB于点F.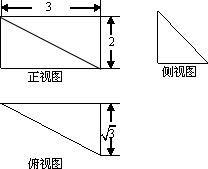 某多面体的三视图如图所示,则该多面体最长的棱长为4;外接球的体积为$\frac{32π}{3}$.
某多面体的三视图如图所示,则该多面体最长的棱长为4;外接球的体积为$\frac{32π}{3}$.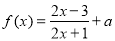 在
在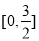 的值域为集合
的值域为集合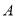 ,函数
,函数 的定义域为集合
的定义域为集合 .
.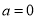 ,求
,求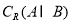 ;
;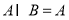 ,求实数
,求实数 的取值范围.
的取值范围.