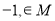题目内容
9.已知三棱锥V-ABC的顶点都在球O的球面上,AB=3,AC=4,AB⊥AC,VA=VB=VC=5,则球O的半径为$\frac{5\sqrt{3}}{3}$.分析 画出图形,判断VBC与平面ABC的关系,找出球心所在位置求解即可.
解答 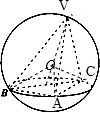 解:如图,AB=3,AC=4,AB⊥AC,说明△ABC是直角三角形,BC=5,是球的小圆的直径,VA=VB=VC=5,可得平面VBC⊥平面ABC,是球的大圆,球心是△VBC的外心,而△VBC是正三角形,边长为5,所以所求球的半径为:$\frac{2}{3}×\sqrt{{5}^{2}-(\frac{5}{2})^{2}}$=$\frac{5\sqrt{3}}{3}$.
解:如图,AB=3,AC=4,AB⊥AC,说明△ABC是直角三角形,BC=5,是球的小圆的直径,VA=VB=VC=5,可得平面VBC⊥平面ABC,是球的大圆,球心是△VBC的外心,而△VBC是正三角形,边长为5,所以所求球的半径为:$\frac{2}{3}×\sqrt{{5}^{2}-(\frac{5}{2})^{2}}$=$\frac{5\sqrt{3}}{3}$.
故答案为:$\frac{5\sqrt{3}}{3}$.
点评 本题考查球的内接体,球的半径的求法,考查计算能力以及空间想象能力.

练习册系列答案
相关题目
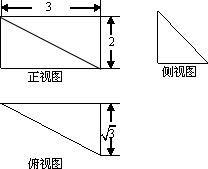 某多面体的三视图如图所示,则该多面体最长的棱长为4;外接球的体积为$\frac{32π}{3}$.
某多面体的三视图如图所示,则该多面体最长的棱长为4;外接球的体积为$\frac{32π}{3}$.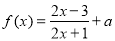 在
在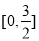 的值域为集合
的值域为集合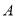 ,函数
,函数 的定义域为集合
的定义域为集合 .
.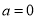 ,求
,求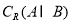 ;
;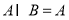 ,求实数
,求实数 的取值范围.
的取值范围.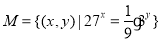 ,则下列说法正确的是( )
,则下列说法正确的是( )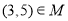 B.
B.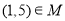
 D.
D.