��Ŀ����
4��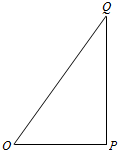 ��ͼ��O��P��Q������ֱ����ͨ��OP=3ǧ�ף�PQ=4ǧ�ף�OQ=5ǧ�ף��ּס�������Աͬʱ��O�س�������ǰ��Q�أ�����tСʱ������֮��ľ���Ϊf��t������λ��ǧ�ף�����·����OQ���ٶ�Ϊ5ǧ��/Сʱ���ҵ�·����OPQ���ٶ�Ϊ8ǧ��/Сʱ���ҵ���Q�غ���ԭ�صȴ�����t=t1ʱ�ҵ���P�أ�t=t2ʱ�ҵ���Q�أ�
��ͼ��O��P��Q������ֱ����ͨ��OP=3ǧ�ף�PQ=4ǧ�ף�OQ=5ǧ�ף��ּס�������Աͬʱ��O�س�������ǰ��Q�أ�����tСʱ������֮��ľ���Ϊf��t������λ��ǧ�ף�����·����OQ���ٶ�Ϊ5ǧ��/Сʱ���ҵ�·����OPQ���ٶ�Ϊ8ǧ��/Сʱ���ҵ���Q�غ���ԭ�صȴ�����t=t1ʱ�ҵ���P�أ�t=t2ʱ�ҵ���Q�أ���1����t1��f��t1����ֵ��
��2����֪��Ա�ĶԽ�������Чͨ��������3ǧ�ף���t1��t��t2ʱ����f��t���ı���ʽ�����ж�f��t����[t1��t2]�ϵ����ֵ�Ƿ�3��˵�����ɣ�
���� ��1����OP���ȳ����ҵ��ٶȼ������t1=$\frac{3}{8}$�����ҵ���P��ʱ���������A�㣬����AP�����ڡ�AOP�и������Ҷ����������AP��Ҳ�͵ó�f��t1����
��2�����t2=$\frac{7}{8}$����t$��[\frac{3}{8}��\frac{7}{8}]$����tСʱ�����B�أ����ҵ���C�أ�������BC���ܹ���t��ʾ��BQ��CQ������֪��cos$��OQP=\frac{4}{5}$�������������Ҷ����������BC����f��t����Ȼ����ú��������ֵ�����Ƿ�3���ɣ�
��� �⣺��1����������֪${t}_{1}=\frac{3}{8}$�����ʱ����A�㣬������AP����ͼ��ʾ����OA=$5��\frac{3}{8}=\frac{15}{8}$��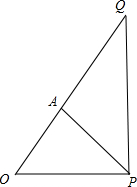 ���ڡ�OAP�������Ҷ����ã�f��t1��=AP=$\sqrt{O{A}^{2}+O{P}^{2}-2OA•OP•cos��AOP}$=$\sqrt{��\frac{15}{8}��^{2}+9-\frac{45}{4}•\frac{3}{5}}=\frac{3\sqrt{41}}{8}$��ǧ�ף���
���ڡ�OAP�������Ҷ����ã�f��t1��=AP=$\sqrt{O{A}^{2}+O{P}^{2}-2OA•OP•cos��AOP}$=$\sqrt{��\frac{15}{8}��^{2}+9-\frac{45}{4}•\frac{3}{5}}=\frac{3\sqrt{41}}{8}$��ǧ�ף���
��2���������${t}_{2}=\frac{7}{8}$����tСʱ����$\frac{3}{8}��t��\frac{7}{8}$��������B�㣬�ҵ�����C�㣬��ͼ��ʾ��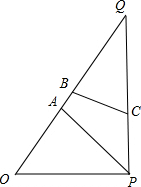 ��BQ=5-5t��CQ=7-8t��
��BQ=5-5t��CQ=7-8t��
���ڡ�BCQ�������Ҷ����ã�f��t��=BC=$\sqrt{��5-5t��^{2}+��7-8t��^{2}-2��5-5t����7-8t��•\frac{4}{5}}$=$\sqrt{25{t}^{2}-42t+18}$��
��f��t��=$\sqrt{25{t}^{2}-42t+18}$��$\frac{3}{8}��t��\frac{7}{8}$��
��g��t��=25t2-42t+18��$\frac{3}{8}��t��\frac{7}{8}$��g��t���ĶԳ���Ϊt=$\frac{21}{25}$$��[\frac{3}{8}��\frac{7}{8}]$��
��$g��\frac{3}{8}��=\frac{369}{64}��g��\frac{7}{8}��=\frac{25}{64}$��
��g��t�������ֵΪ$\frac{369}{64}$�����ʱf��t��ȡ���ֵ$\frac{3\sqrt{41}}{8}��3$��
��f��t����[t1��t2]�ϵ����ֵ������3��
���� �������Ҷ�����Ӧ�ã��Լ����κ����ڱ���������ֵ����

 ��������ABCD-A1B1C1D1�У�AA1��ƽ��A1B1C1D1������A1B1C1D1�DZ߳�Ϊa�������Σ�����AA1�ij�Ϊb��EΪ����BB1�ϵĶ��㣨�����˵㣩��������
��������ABCD-A1B1C1D1�У�AA1��ƽ��A1B1C1D1������A1B1C1D1�DZ߳�Ϊa�������Σ�����AA1�ij�Ϊb��EΪ����BB1�ϵĶ��㣨�����˵㣩��������| A�� | �������a��b�����ڵ�E��ʹ��B1D��EC1 | |
| B�� | ���ҽ���a=bʱ�����ڵ�E��ʹ��B1D��EC1 | |
| C�� | ���ҽ���a��bʱ�����ڵ�E��ʹ��B1D��EC1 | |
| D�� | ���ҽ���a��bʱ�����ڵ�E��ʹ��B1D��EC1 |
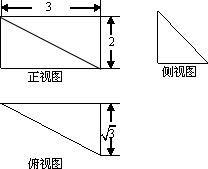 ij�����������ͼ��ͼ��ʾ����ö���������ⳤΪ4�����������Ϊ$\frac{32��}{3}$��
ij�����������ͼ��ͼ��ʾ����ö���������ⳤΪ4�����������Ϊ$\frac{32��}{3}$�� ��ͼ��������C1��x2=2py��p��0���Ľ���ΪF����ԲC2��$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=l ��a��b��0����������e=$\frac{\sqrt{3}}{2}$��C1��C2�ڵ�һ���Ľ���ΪP��2��1����
��ͼ��������C1��x2=2py��p��0���Ľ���ΪF����ԲC2��$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=l ��a��b��0����������e=$\frac{\sqrt{3}}{2}$��C1��C2�ڵ�һ���Ľ���ΪP��2��1����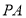 ��Բ���ڵ�
��Բ���ڵ�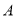 ����
����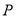 ��ֱ����Բ����
��ֱ����Բ���� ���㣬��
���㣬��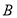 ��Բ�ϣ���
��Բ�ϣ���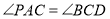 ��
��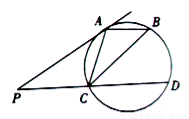
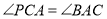 ��
��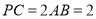 ����
���� ��
��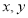 ��������
�������� ����
����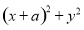 ����СֵΪ6��
����СֵΪ6��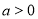 ����
���� _____________��
_____________��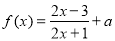 ��
��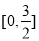 ��ֵ��Ϊ����
��ֵ��Ϊ����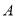 ������
������ �Ķ�����Ϊ����
�Ķ�����Ϊ���� .
.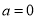 ����
����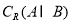 ��
��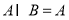 ����ʵ��
����ʵ�� ��ȡֵ��Χ.
��ȡֵ��Χ.