题目内容
7.已知函数f(x)=x2-(k+1)x+$\frac{9}{4}$,g(x)=2x-k,其中k∈R(1)若f(x)在区间(1,4)上有零点,求实数k的取值范围;
(2)设函数p(x)=$\left\{\begin{array}{l}{f(x),x<0}\\{g(x),x≥0}\end{array}\right.$,是否存在实数k,对任意给定的非零实数x1,存在唯一的非零实数x2(x1≠x2),使得p(x1)=p(x2)?若存在,求出k的值,若不存在,请说明理由.
分析 (1)由题意可得△=(k+4)(k-2),分类讨论,分别求出实数k的取值范围,再取并集,即得所求.
(2)根据g(x)在(0,+∞)单调递增,其值域为(-k,+∞),f(x)在(-∞,0)上的值域为($\frac{9}{4}$,+∞),即可得出结论.
解答 解:(1)由题意知△=(k+4)(k-2)…(2分)
①当f(1)f(4)<0时,$\frac{9}{4}<k<\frac{57}{16}$.…(3分)
②当f(1)f(4)=0时,k=$\frac{9}{4}$或k=$\frac{57}{16}$,经检验k=$\frac{9}{4}$符合.…(4分)
③当△=0时,k=2或k=-4,经检验k=2符合.…(5分)
④当$\left\{\begin{array}{l}{△>0}\\{1<\frac{k+1}{2}<4}\\{f(1)>0}\\{f(4)>0}\end{array}\right.$时,解得2<k<$\frac{9}{4}$.…(6分)
综上2≤k<$\frac{57}{16}$ …(8分)
(Ⅱ)显然g(x)在(0,+∞)单调递增,其值域为(-k,+∞) …(10分)
∴f(x)在(-∞,0)上单调递减,$\frac{k+1}{2}$≥0即k≥-1.
∴f(x)在(-∞,0)上的值域为($\frac{9}{4}$,+∞) …(12分)
∴$k=-\frac{9}{4}$
而 k≥-1,∴这样的k不存在. …(14分)
点评 本题主要考查函数的零点与方程的根的关系,函数的单调性的应用,体现了化归与转化、以及分类讨论的数学思想,属于中档题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
19.设等差数列{an}的前n项和为Sn,已知(a7-1)3+2012(a7-1)=1,(a2006-1)3+2012(a2006-1)=-1,则下列结论正确的是( )
| A. | S2012=-2012,a2012>a7 | B. | S2012=2012,a2012>a7 | ||
| C. | S2012=-2012,a2012<a7 | D. | S2012=2012,a2012<a7 |
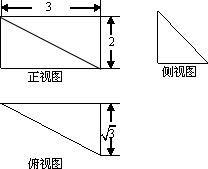 某多面体的三视图如图所示,则该多面体最长的棱长为4;外接球的体积为$\frac{32π}{3}$.
某多面体的三视图如图所示,则该多面体最长的棱长为4;外接球的体积为$\frac{32π}{3}$. 如图,抛物线C1:x2=2py(p>0)的焦点为F,椭圆C2:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=l (a>b>0)的离心率e=$\frac{\sqrt{3}}{2}$,C1与C2在第一象限的交点为P(2,1).
如图,抛物线C1:x2=2py(p>0)的焦点为F,椭圆C2:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=l (a>b>0)的离心率e=$\frac{\sqrt{3}}{2}$,C1与C2在第一象限的交点为P(2,1).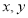 满足条件
满足条件 ,且
,且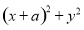 的最小值为6,
的最小值为6,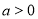 ,则
,则 _____________.
_____________.