题目内容
20. Rt△ABC中,∠C=90°,CD⊥AB,AD为圆O的直径,圆O与AC交于E,求证:$\frac{AE}{CE}$=$\frac{A{C}^{2}}{B{C}^{2}}$.
Rt△ABC中,∠C=90°,CD⊥AB,AD为圆O的直径,圆O与AC交于E,求证:$\frac{AE}{CE}$=$\frac{A{C}^{2}}{B{C}^{2}}$.
分析 连接DE,利用射影定理,结合平行线分线段成比例,即可证明结论.
解答 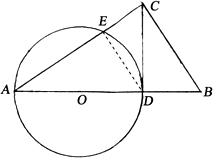 解:连接DE,
解:连接DE,
因为Rt△ABC中,∠C=90°,CD⊥AB,
所以BC2=BD•BA,AC2=AD•BD,
所以$\frac{A{C}^{2}}{B{C}^{2}}$=$\frac{AD}{BD}$,
因为DE⊥AE,BC⊥AC,
所以DE∥BC,
所以$\frac{AE}{CE}$=$\frac{AD}{BD}$,
所以:$\frac{AE}{CE}$=$\frac{A{C}^{2}}{B{C}^{2}}$.
点评 本题考查射影定理,平行线分线段成比例定理,考查学生分析解决问题的能力,比较基础.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
13.已知数列{an}满足a1=3,且an+1=4an+3(n∈N*),则数列{an}的通项公式为( )
| A. | 22n-1+1 | B. | 22n-1-1 | C. | 22n+1 | D. | 22n-1 |
 如图,在三棱锥P-ABC中,△ABC是边长为2的正三角形,∠PCA=90°,E,H分别为AP,AC的中点,AP=4,BE=$\sqrt{3}$.
如图,在三棱锥P-ABC中,△ABC是边长为2的正三角形,∠PCA=90°,E,H分别为AP,AC的中点,AP=4,BE=$\sqrt{3}$. 如图:⊙O的直径AB的延长线于弦CD的延长线相交于点P,E为⊙O上一点,$\widehat{AE}$=$\widehat{AC}$,DE交AB于点F.
如图:⊙O的直径AB的延长线于弦CD的延长线相交于点P,E为⊙O上一点,$\widehat{AE}$=$\widehat{AC}$,DE交AB于点F.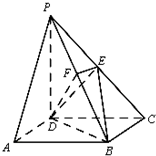 如图所示,在四棱锥P-ABCD中,底面ABCD是矩形,侧棱PD⊥底面ABCD,PD=DC,E是PC的中点,作EF⊥PB交PB于点F.
如图所示,在四棱锥P-ABCD中,底面ABCD是矩形,侧棱PD⊥底面ABCD,PD=DC,E是PC的中点,作EF⊥PB交PB于点F.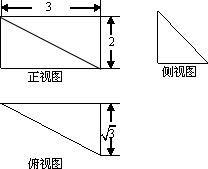 某多面体的三视图如图所示,则该多面体最长的棱长为4;外接球的体积为$\frac{32π}{3}$.
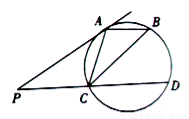
某多面体的三视图如图所示,则该多面体最长的棱长为4;外接球的体积为$\frac{32π}{3}$.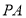 与圆切于点
与圆切于点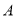 ,过
,过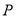 作直线与圆交于
作直线与圆交于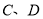 两点,点
两点,点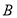 在圆上,且
在圆上,且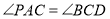 .
.
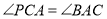 ;
;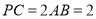 ,求
,求 .
.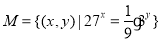 ,则下列说法正确的是( )
,则下列说法正确的是( )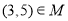 B.
B.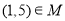
 D.
D.