题目内容
17.已知函数f(x)=$\frac{1}{x+2}$-k|x|({k∈R})有三个不同的零点,则实数k的取值范围是( )| A. | (0,1) | B. | (0,2) | C. | (1,+∞) | D. | (2,+∞) |
分析 把函数的零点转化为两个函数图象交点的横坐标,由题意画出图形,数形结合得到实数k的取值范围.
解答 解:如图,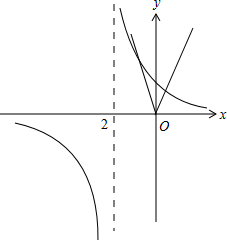 函数f(x)=$\frac{1}{x+2}$-k|x|的零点,就是方程$\frac{1}{x+2}$-k|x|=0的根,
函数f(x)=$\frac{1}{x+2}$-k|x|的零点,就是方程$\frac{1}{x+2}$-k|x|=0的根,
也就是函数$y=\frac{1}{x+2}$与函数$y=k|x|=\left\{\begin{array}{l}{kx,x≥0}\\{-kx,x<0}\end{array}\right.$图象交点的横坐标.
若k=0,则y=k|x|=0,函数$y=\frac{1}{x+2}$与y=0无交点;
若k<0,则当x>0时,y=kx与$y=\frac{1}{x+2}$无交点,不合题意;
当k>0时,y=kx与$y=\frac{1}{x+2}$右支有一个交点,
再由$\left\{\begin{array}{l}{y=\frac{1}{x+2}}\\{y=-kx}\end{array}\right.$,得kx2+2kx+1=0,由△=4k2-4k=0,得k=1.
由图可知,当k>1时y=-kx与$y=\frac{1}{x+2}$左支有两个交点.
∴使函数f(x)=$\frac{1}{x+2}$-k|x|({k∈R})有三个不同的零点的实数k的取值范围是(1,+∞).
故选:C.
点评 本题考查了函数的零点和方程根的关系,考查了数形结合的解题思想方法,考查了数学转化思想方法,是中档题.

练习册系列答案
相关题目
 如图:⊙O的直径AB的延长线于弦CD的延长线相交于点P,E为⊙O上一点,$\widehat{AE}$=$\widehat{AC}$,DE交AB于点F.
如图:⊙O的直径AB的延长线于弦CD的延长线相交于点P,E为⊙O上一点,$\widehat{AE}$=$\widehat{AC}$,DE交AB于点F.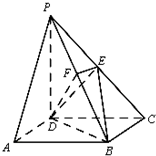 如图所示,在四棱锥P-ABCD中,底面ABCD是矩形,侧棱PD⊥底面ABCD,PD=DC,E是PC的中点,作EF⊥PB交PB于点F.
如图所示,在四棱锥P-ABCD中,底面ABCD是矩形,侧棱PD⊥底面ABCD,PD=DC,E是PC的中点,作EF⊥PB交PB于点F.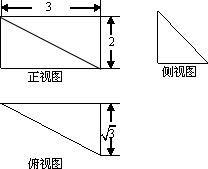 某多面体的三视图如图所示,则该多面体最长的棱长为4;外接球的体积为$\frac{32π}{3}$.
某多面体的三视图如图所示,则该多面体最长的棱长为4;外接球的体积为$\frac{32π}{3}$.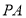 与圆切于点
与圆切于点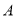 ,过
,过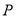 作直线与圆交于
作直线与圆交于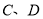 两点,点
两点,点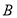 在圆上,且
在圆上,且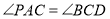 .
.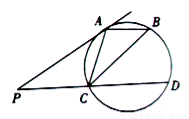
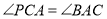 ;
;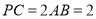 ,求
,求 .
.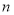 的值是( )
的值是( )