题目内容
5.设m,n是两条不同的直线,α,β是两个不同的平面,则( )| A. | 若m∥α,m∥β,则α∥β | B. | 若m∥α,m∥n,则n∥α | C. | 若m⊥α,m∥β,则α⊥β | D. | 若m∥α,n?α,则m∥n |
分析 A.若m∥α,m∥β,则α∥β,可由面面平行的条件判断;
B.m∥α,m∥n,则n∥α,或n?α;
C.若m⊥α,m∥β,则α⊥β,可由面面垂直的判断定理作出判断;
D.m∥α,n?α,则m∥n或m,n异面.
解答 解:A.若m∥α,m∥β,则α∥β;此命题错误,因为两个平面平行于同一条直线不能保证两个平面平行,故不正确;
B.m∥α,m∥n,则n∥α,或n?α,故不正确;
C.若m⊥α,m∥β,则α⊥β;此命题正确,因为m∥β,则一定存在直线n在β,使得m∥n,又m⊥α可得出n⊥α,由面面垂直的判定定理知,α⊥β,正确;
D.m∥α,n?α,则m∥n或m,n异面,故不正确.
故选:C.
点评 本题考查平面与平面之间的位置关系,空间中两个平面的位置关系主要有相交与平行,相交中比较重要的位置关系是两面垂直,本题考查了利用基础理论作出推理判断的能力,是立体几何中的基本.

练习册系列答案
 小学生10分钟口算测试100分系列答案
小学生10分钟口算测试100分系列答案
相关题目
13.已知数列{an}满足a1=3,且an+1=4an+3(n∈N*),则数列{an}的通项公式为( )
| A. | 22n-1+1 | B. | 22n-1-1 | C. | 22n+1 | D. | 22n-1 |
16. 在四棱柱ABCD-A1B1C1D1中,AA1⊥平面A1B1C1D1,底面A1B1C1D1是边长为a的正方形,侧棱AA1的长为b,E为侧棱BB1上的动点(包括端点),则( )
在四棱柱ABCD-A1B1C1D1中,AA1⊥平面A1B1C1D1,底面A1B1C1D1是边长为a的正方形,侧棱AA1的长为b,E为侧棱BB1上的动点(包括端点),则( )
 在四棱柱ABCD-A1B1C1D1中,AA1⊥平面A1B1C1D1,底面A1B1C1D1是边长为a的正方形,侧棱AA1的长为b,E为侧棱BB1上的动点(包括端点),则( )
在四棱柱ABCD-A1B1C1D1中,AA1⊥平面A1B1C1D1,底面A1B1C1D1是边长为a的正方形,侧棱AA1的长为b,E为侧棱BB1上的动点(包括端点),则( )| A. | 对任意的a,b,存在点E,使得B1D⊥EC1 | |
| B. | 当且仅当a=b时,存在点E,使得B1D⊥EC1 | |
| C. | 当且仅当a≤b时,存在点E,使得B1D⊥EC1 | |
| D. | 当且仅当a≥b时,存在点E,使得B1D⊥EC1 |
 ,
, ,
, ,
, ,依照以上各式成立的规律,得到一般性的等式为( )
,依照以上各式成立的规律,得到一般性的等式为( ) B.
B.
 D.
D.
 如图,在三棱锥P-ABC中,△ABC是边长为2的正三角形,∠PCA=90°,E,H分别为AP,AC的中点,AP=4,BE=$\sqrt{3}$.
如图,在三棱锥P-ABC中,△ABC是边长为2的正三角形,∠PCA=90°,E,H分别为AP,AC的中点,AP=4,BE=$\sqrt{3}$.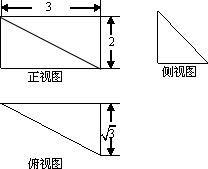 某多面体的三视图如图所示,则该多面体最长的棱长为4;外接球的体积为$\frac{32π}{3}$.
某多面体的三视图如图所示,则该多面体最长的棱长为4;外接球的体积为$\frac{32π}{3}$.