题目内容
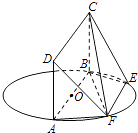
【题目】如图，在正方体
中，
分别是
中点.
求证：（1）
∥平面
；
（2）
平面.
【答案】（1）详见解析（2）详见解析
【解析】
试题分析：
（1）利用正方体的性质和三角形中位线性质可得EF∥AD1，进而利用平行四边形ABC1D1转化为EF∥BC1，最后利用线面平行的判定定理证得结论．
（2）首先利用侧棱垂直于底面得到AA1⊥BD，然后结合正方形性质有AC⊥BD即可证得BD⊥平面AA1C，同理可证A1C⊥BC1最后利用线面垂直的判定定理即得结论．
试题解析：
证明：（1）连结A1D，
∵ E，F分别是AD和DD1的中点，∴ EF∥AD1 ． 2分
∵ 正方体ABCD－A1B1C1D1，
∴ AB∥D1C1，AB=D1C1．
∴ 四边形ABC1D1为平行四边形，即有A1D∥BC1 4分
∴ EF∥BC1．
又EF
平面C1BD，BC1
平面C1BD，
∴ EF∥平面AB1D1． 7分
（2）连结AC，则AC⊥BD．
∵ 正方体ABCD－A1B1C1D1，∴AA1⊥平面ABCD，
∴ AA1⊥BD．
又
，∴BD⊥平面AA1C，
∴ A1C⊥BD． 11分
同理可证A1C⊥BC1．
又
，∴A1C⊥平面C1BD． 14分
练习册系列答案
相关题目
【题目】某个体服装店经营某种服装，在某周内获纯利y（元）与该周每天销售这种服装件数x之间的一组数据关系如下表
x | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
y | 66 | 69 | 73 | 81 | 89 | 90 | 91 |
（1）求纯利y与每天销售件数x之间的回归方程；
（2）若该周内某天销售服装20件，估计可获纯利多少元？
已知： 
x 
=280， y =45309， xiyi=3487， 
= 
， 
= 
﹣ 
．
