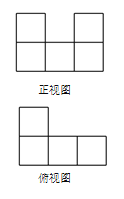
题目内容
【题目】已知函数 ![]() .
.
(1)求函数 ![]() 的单调区间和极值;
的单调区间和极值;
(2)是否存在实数 ![]() ,使得函数
,使得函数 ![]() 在
在 ![]() 上的最小值为
上的最小值为 ![]() ?若存在,求出
?若存在,求出 ![]() 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.
【答案】
(1)解:由题意知, ![]() .
.
由 ![]() 得
得 ![]() ,解得
,解得 ![]() ,所以函数
,所以函数 ![]() 的单调增区间是
的单调增区间是 ![]() ;
;
由 ![]() 得
得 ![]() ,解得
,解得 ![]() ,所以函数
,所以函数 ![]() 的单调减区间是
的单调减区间是 ![]() .
. ![]() 当
当 ![]() 时,函数
时,函数 ![]() 有极小值为
有极小值为 ![]()
(2)解:由(1)可知,当 ![]() 时,
时, ![]() 单调递减,当
单调递减,当 ![]() 时,
时, ![]() 单调递增.
单调递增.
①若 ![]() ,即
,即 ![]() 时,函数
时,函数 ![]() 在
在 ![]() 上为增函数,故函数
上为增函数,故函数 ![]() 的最小值为
的最小值为 ![]() ,显然
,显然 ![]() ,故不满足条件.
,故不满足条件.
②若 ![]() ,即
,即 ![]() 时,函数
时,函数 ![]() 在
在 ![]() 上为减函数,在
上为减函数,在 ![]() 上为增函数,故函数
上为增函数,故函数 ![]() 的最小值为
的最小值为 ![]() ,即
,即 ![]() ,解得
,解得 ![]() ,而
,而 ![]() ,故不满足条件.
,故不满足条件.
③若 ![]() ,即
,即 ![]() 时,函数
时,函数 ![]() 在在
在在 ![]() 上为减函数,故函数
上为减函数,故函数 ![]() 的最小值为
的最小值为 ![]() ,即
,即 ![]() ,而
,而 ![]() 不满足条件,综上所述,这样的
不满足条件,综上所述,这样的 ![]() 不存在
不存在
【解析】(1)根据题意求出原函数的导函数再利用导函数的正负得出原函数的增减性。(2)首先求出原函数的导函数由导函数大于零解出x的取值范围然后对a分三种情况讨论,再利用f ( x ) 在 [ 1 , e ] 上的最小值为 0求出a的值即可。
【考点精析】解答此题的关键在于理解利用导数研究函数的单调性的相关知识,掌握一般的,函数的单调性与其导数的正负有如下关系: 在某个区间![]() 内,(1)如果
内,(1)如果![]() ,那么函数
,那么函数![]() 在这个区间单调递增;(2)如果
在这个区间单调递增;(2)如果![]() ,那么函数
,那么函数![]() 在这个区间单调递减,以及对函数的极值与导数的理解,了解求函数
在这个区间单调递减,以及对函数的极值与导数的理解,了解求函数![]() 的极值的方法是:(1)如果在
的极值的方法是:(1)如果在![]() 附近的左侧
附近的左侧![]() ,右侧
,右侧![]() ,那么
,那么![]() 是极大值(2)如果在
是极大值(2)如果在![]() 附近的左侧
附近的左侧![]() ,右侧
,右侧![]() ,那么
,那么![]() 是极小值.
是极小值.

【题目】假设关于某种设备的使用年限![]() (年)与所支出的维修费用
(年)与所支出的维修费用![]() (万元)有如下统计资料:
(万元)有如下统计资料:
x | 2 | 3 | 4 | 5 | 6 |
y | 2.2 | 3.8 | 5.5 | 6.5 | 7.0 |
已知![]() ,
, ![]() .
.
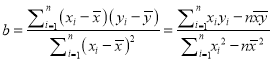 ,
, ![]()
(1)求![]() ,
, ![]() ;
;
(2) ![]() 与
与![]() 具有线性相关关系,求出线性回归方程;
具有线性相关关系,求出线性回归方程;
(3)估计使用年限为10年时,维修费用约是多少?