Question

【题目】德国数学家科拉茨1937年提出一个著名的猜想：任给一个正整数 ，如果 是偶数，就将它减半（即 ）；如果 是奇数，则将它乘3加1（即 ），不断重复这样的运算，经过有限步后，一定可以得到1.对于科拉茨猜想，目前谁也不能证明。也不能否定，现在请你研究：如果对正整数 （首项）按照上述规则旅行变换后的第9项为1（注：1可以多次出现），则 的所有不同值的个数为 ．

Answer 1

【答案】7
【解析】如果正整数 按照上述规则施行变换后的第9项为1，则变换中的第8项一定是2，变换中的第7项一定是4；按照这种逆推的对应关系可得如下树状图： ，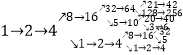

则 的所有可能的取值为4，5， 6，32，40，42，256共7个，所以答案是7.