题目内容
已知直线l是过点P(-1,2),方向向量为
=(-1,
)的直线,圆方程ρ=2cos(θ+
)
(1)求直线l的参数方程
(2)设直线l与圆相交于M,N两点,求|PM|•|PN|的值.
| n |
| 3 |
| π |
| 3 |
(1)求直线l的参数方程
(2)设直线l与圆相交于M,N两点,求|PM|•|PN|的值.
(1)∵
=(-1,
),∴直线的倾斜角α=
,
∴直线的参数方程为
,(t为参数)
即
(t为参数)
(2)∵ρ=2(
cosθ+
sinθ)=cosθ+
sinθ,
∴ρ2=ρcosθ+
ρsinθ,
∴x2+y2-x-
y=0,将直线的参数方程代入得t2+2
t+6-2
=0,
∴|t1t2|=6-2
.
| n |
| 3 |
| 2π |
| 3 |
∴直线的参数方程为
|
即
|
(2)∵ρ=2(
| 1 |
| 2 |
| ||
| 2 |
| 3 |
∴ρ2=ρcosθ+
| 3 |
∴x2+y2-x-
| 3 |
| 3 |
| 3 |
∴|t1t2|=6-2
| 3 |

练习册系列答案
相关题目
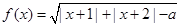 .
.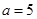 ,求函数
,求函数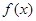 的定义域
的定义域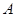 ;
;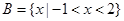 ,当实数
,当实数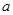 ,
,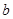
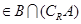 时,求证:
时,求证: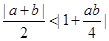 .
.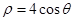 上的点到直线
上的点到直线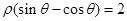 的最大距离为 .
的最大距离为 .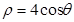 的圆心到直线
的圆心到直线 的距离为 .
的距离为 .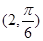 到直线
到直线 的距离是
的距离是 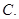
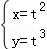 (t为参数)相交于A,B两点,则|AB|= _________ .
(t为参数)相交于A,B两点,则|AB|= _________ .