题目内容
在直角坐标系中,直线l经过点P(3,0),倾斜角α=
.
(1)写出直线l的参数方程;
(2)以原点为极点,x轴的正半轴为极轴建立极坐标系,已知曲线C:ρ=4cosθ与直线l相交于A、B两点,求AB中点坐标及点P到A、B两点距离之积.
| π |
| 4 |
(1)写出直线l的参数方程;
(2)以原点为极点,x轴的正半轴为极轴建立极坐标系,已知曲线C:ρ=4cosθ与直线l相交于A、B两点,求AB中点坐标及点P到A、B两点距离之积.
(1)由于直线l经过点P(3,0),倾斜角α=
.
故直线l的参数方程为
,即
(t为参数);
(2)∵C:ρ=4cosθ,∴x2+y2=4x,
将
(t为参数)代入x2+y2=4x
整理得t2+
t-3=0,
∵△>0,∴t1+t2=-
,即
=-
代入
(t为参数)
得AB中点坐标为(
,-
),
故P到A、B两点距离之积为|t1•t2|=3.
| π |
| 4 |
故直线l的参数方程为
|
|
(2)∵C:ρ=4cosθ,∴x2+y2=4x,
将
|
整理得t2+
| 2 |
∵△>0,∴t1+t2=-
| 2 |
| t1+t2 |
| 2 |
| ||
| 2 |
代入
|
得AB中点坐标为(
| 5 |
| 2 |
| 1 |
| 2 |
故P到A、B两点距离之积为|t1•t2|=3.

练习册系列答案
相关题目
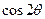 ,给定两点P(0,π/2),Q(-2,π),则有 ( )
,给定两点P(0,π/2),Q(-2,π),则有 ( ) 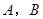 分别是直线
分别是直线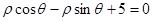 和
和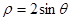 上的动点,则
上的动点,则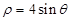 相切的一条直线的方程为( )
相切的一条直线的方程为( )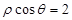
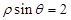
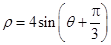
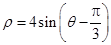
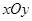 中,已知曲线
中,已知曲线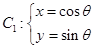 (
(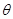 为参数),将曲线
为参数),将曲线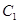 上的所有点的横坐标、纵坐标分别伸长为原来的
上的所有点的横坐标、纵坐标分别伸长为原来的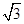 、
、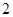 倍后得到曲线
倍后得到曲线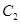 的直角坐标方程为 .
的直角坐标方程为 .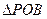 中,
中,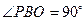 ,以
,以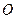 为圆心、
为圆心、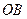 为半径作圆弧交
为半径作圆弧交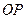 于
于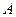 点.若弧AB等分△POB的面积,且∠AOB=
点.若弧AB等分△POB的面积,且∠AOB=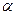 弧度,则( )
弧度,则( )