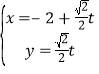题目内容
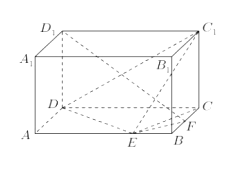
【题目】在如图所示的几何体中,四边形![]() 是正方形,
是正方形,![]() 平面
平面![]() ,
,![]() 、
、![]() 分别是线段
分别是线段![]() 、
、![]() 的中点,
的中点,![]() .
.

(1)证明:![]() 平面
平面![]() ;
;
(2)设点![]() 是线段
是线段![]() 的中点,求二面角
的中点,求二面角![]() 的余弦值.
的余弦值.
【答案】(1)证明见解析;(2)![]() .
.
【解析】
(1)取![]() 的中点
的中点![]() ,连接
,连接![]() 、
、![]() ,证明出四边形
,证明出四边形![]() 为平行四边形,可得出
为平行四边形,可得出![]() ,然后利用直线与平面平行的判定定理可证明出
,然后利用直线与平面平行的判定定理可证明出![]() 平面
平面![]() ;
;
(2)以点![]() 为坐标原点,分别以
为坐标原点,分别以![]() 、
、![]() 、
、![]() 所在直线为
所在直线为![]() 轴、
轴、![]() 轴、
轴、![]() 轴建立空间直角坐标系,计算出平面
轴建立空间直角坐标系,计算出平面![]() 和平面
和平面![]() 的法向量,然后利用空间向量法可求出二面角
的法向量,然后利用空间向量法可求出二面角![]() 的余弦值.
的余弦值.
(1)取![]() 的中点为
的中点为![]() ,连接
,连接![]() 、
、![]() ,如图:
,如图:
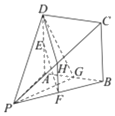
![]() 四边形
四边形![]() 为正方形,
为正方形,![]() 、
、![]() 、
、![]() 分别是线段
分别是线段![]() 、
、![]() 、
、![]() 的中点,
的中点,
![]() 且
且![]() ,
,![]() 且
且![]() ,
,![]() ,
,
![]() 四边形
四边形![]() 为平行四边形,
为平行四边形,![]() ,
,
![]() 平面
平面![]() ,
,![]() 平面
平面![]() ,
,![]() 平面
平面![]() ;
;
(2)![]() 平面
平面![]() ,四边形
,四边形![]() 是正方形,
是正方形,![]() 、
、![]() 、
、![]() 两两垂直,
两两垂直,
以点![]() 为坐标原点,分别以
为坐标原点,分别以![]() 、
、![]() 、
、![]() 所在直线为
所在直线为![]() 轴、
轴、![]() 轴、
轴、![]() 轴建立空间直角坐标系,则
轴建立空间直角坐标系,则![]() 、
、![]() 、
、![]() 、
、![]() ,
,
![]() ,
,![]() ,
,![]() ,
,
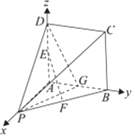
设平面![]() 的法向量为
的法向量为![]() ,则
,则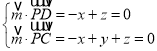 ,
,
取![]() ,则
,则![]() ,
,![]() ,则平面
,则平面![]() 的一个法向量为
的一个法向量为![]() ,
,
设平面![]() 的法向量为
的法向量为![]() ,则
,则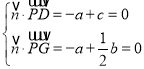 ,
,
取![]() ,则
,则![]() ,
,![]() ,则平面
,则平面![]() 的一个法向量为
的一个法向量为![]() .
.
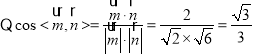 ,
,
由图形可知,二面角![]() 为锐角,其余弦值为
为锐角,其余弦值为![]() .
.

 暑假作业暑假快乐练西安出版社系列答案
暑假作业暑假快乐练西安出版社系列答案【题目】为了解人们对于国家新颁布的“生育二胎放开”政策的热度,现在某市进行调查,随机调查了50人,他们年龄大点频率分布及支持“生育二胎”人数如下表:
年龄 |
|
|
|
|
|
|
频率 | 5 | 10 | 15 | 10 | 5 | 5 |
支持“生育二胎” | 4 | 5 | 12 | 8 | 2 | 1 |
(1)由以上统计数据填下面2乘2列联表,并问是否有99%的把握认为以45岁为分界点对“生育二胎放开”政策的支持度有差异:

(2)若对年龄在![]() 的被调查人中随机选取两人进行调查,恰好这两人都支持“生育二胎放开”的概率是多少?
的被调查人中随机选取两人进行调查,恰好这两人都支持“生育二胎放开”的概率是多少?
参考数据: ![]() ,
, ![]() ,
, ![]() .
.
【题目】随着我国经济的飞速发展,人民生活水平得到很大提高,汽车已经进入千千万万的家庭.大部分的车主在购买汽车时,会在轿车或者![]() 中作出选择,为了研究某地区哪种车型更受欢迎以及汽车一年内的行驶里程,某汽车销售经理作出如下统计:
中作出选择,为了研究某地区哪种车型更受欢迎以及汽车一年内的行驶里程,某汽车销售经理作出如下统计:
购买了轿车(辆) | 购买了 | |
|
|
|
|
|
|
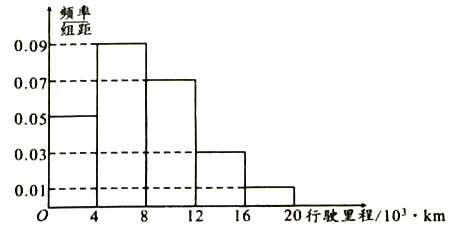
(1)根据表,是否有![]() 的把握认为年龄与购买的汽车车型有关?
的把握认为年龄与购买的汽车车型有关?
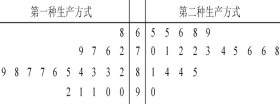
(2)图给出的是![]() 名车主上一年汽车的行驶里程,求这
名车主上一年汽车的行驶里程,求这![]() 名车主上一年汽车的平均行驶里程(同一组中的数据用该组区间的中点值作代表);
名车主上一年汽车的平均行驶里程(同一组中的数据用该组区间的中点值作代表);
(3)用分层抽样的方法从![]() 岁以上车主中抽取
岁以上车主中抽取![]() 人,再从这
人,再从这![]() 人中随机抽取
人中随机抽取![]() 人赠送免费保养券,求这
人赠送免费保养券,求这![]() 人中至少有
人中至少有![]() 辆轿车的概率。
辆轿车的概率。
附:![]() ,
,![]()
|
|
|
|
|
|
|
|
|
|