题目内容
5.在正方体ABCD-A1B1C1D1中,设点P在线段CC1上,直线BP与平面A1BD所成的角为α,则sinα的取值范围是( )| A. | [$\frac{{\sqrt{3}}}{3}$,$\frac{{\sqrt{6}}}{3}$] | B. | [$\frac{\sqrt{6}}{3}$,1] | C. | [$\frac{\sqrt{6}}{3}$,$\frac{2\sqrt{2}}{3}$] | D. | [$\frac{2\sqrt{2}}{2}$,1] |
分析 设正方体的棱长等于1,建立如图空间直角坐标系,得出D、B、C1、A1各点的坐标,从而得出$\overrightarrow{{BC}_{1}}$、$\overrightarrow{{A}_{1}D}$、$\overrightarrow{BD}$ 的坐标,利用垂直向量数量积为零的方法建立方程组解出平面A1BD的一个法向量$\overrightarrow{n}$的坐标,利用向量的夹角公式算出sinθ=|cos<$\overrightarrow{BP}$,$\overrightarrow{n}$>|的值,即得直线BP与平面A1BD所成角的正弦值,根据直线BP与平面A1BD所成角的正弦值的平方的范围,从而得到sinθ的取值范围.
解答 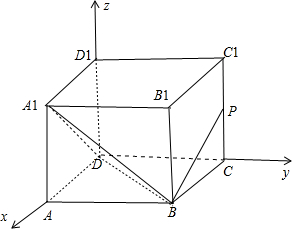 解:分别以DA、DC、DD1为x、y、z轴建立如图
解:分别以DA、DC、DD1为x、y、z轴建立如图
所示空间直角坐标系,
设正方体的棱长等于1,可得
D(0,0,0),B(1,1,0),C1(0,1,1),
A1(1,0,1),
∴$\overrightarrow{{BC}_{1}}$=(-1,0,1),$\overrightarrow{{A}_{1}D}$=(-1,0,-1),
$\overrightarrow{BD}$=(-1,-1,0)
设$\overrightarrow{n}$=(x,y,z)是平面A1BD的一个法向量,
则$\left\{\begin{array}{l}{\overrightarrow{n}•\overrightarrow{{A}_{1}D}=-x-z=0}\\{\overrightarrow{n}•\overrightarrow{BD}=-x-y=0}\end{array}\right.$,取x=1,得y=z=-1,
∴平面A1BD的一个法向量为$\overrightarrow{n}$=(1,-1,-1).
设直线BP与平面A1BD所成角为θ,θ∈( 0,$\frac{π}{2}$],
设P(0,1,m),则由题意可得m∈[0,1],
则sinθ=|cos<$\overrightarrow{BP}$,$\overrightarrow{n}$>|=|$\frac{\overrightarrow{BP}•\overrightarrow{n}}{|\overrightarrow{BP}|•|\overrightarrow{n}|}$|=|$\frac{-m-1}{\sqrt{{m}^{2}+1}•\sqrt{3}}$|=$\frac{m+1}{\sqrt{3}•\sqrt{{m}^{2}+1}}$,
sin2θ=$\frac{{m}^{2}+2m+1}{3{(m}^{2}+1)}$=$\frac{1}{3}$+$\frac{2}{3}$•$\frac{m}{{m}^{2}+1}$,
故sin2θ≥$\frac{1}{3}$,sin2θ≤$\frac{1}{3}$+$\frac{2}{3}$•$\frac{m}{2m}$=$\frac{2}{3}$,即sin2θ∈[$\frac{1}{3}$,$\frac{2}{3}$],
∴sinθ∈[$\frac{\sqrt{3}}{3}$,$\frac{\sqrt{6}}{3}$],
故选:A.
点评 本题给出正方体模型,求直线与平面所成角的余弦值,着重考查了正方体的性质、利用空间向量研究直线与平面所成角等知识,属于中档题.

 阅读快车系列答案
阅读快车系列答案| A. | k≥2 | B. | 0<k≤2 | C. | $k≥\frac{{{e^3}+\sqrt{{e^6}+8}}}{2}$ | D. | $0<k≤\frac{{{e^3}+\sqrt{{e^6}+8}}}{2}$ |
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充要条件 | D. | 既不充分又不必要条件 |
| A. | $\frac{\sqrt{2}}{2}$ | B. | $\sqrt{2}$ | C. | $\frac{\sqrt{3}}{2}$ | D. | $\sqrt{3}$ |
| A. | S10 | B. | S11 | C. | S20 | D. | S21 |
| A. | $\sqrt{3}$ | B. | 4 | C. | $\sqrt{23}$ | D. | 2$\sqrt{6}$ |




