题目内容
【题目】已知函数f(x)=ln(2+ax)(a>0),![]() (b∈R).
(b∈R).
(1)若函数f(x)的图象在点(3,f(3))处的切线与函数g(x)的图象在点(1,g(1))处的切线平行,求a,b之间的关系;
(2)在(1)的条件下,若b=a,且f(x)≥mg(x)对任意x∈[![]() ,+∞)恒成立,求实数m的取值范围.
,+∞)恒成立,求实数m的取值范围.
【答案】(1)![]() (2)(-∞,
(2)(-∞,![]() ]
]
【解析】
(1)对函数求导,再根据在两点处的切线的斜率相等,得到f'(3)=g'(1),进而得到参数的关系;(2)先由b=a求出参数值,令![]() ,则问题转化为h(x)≥0对任意x∈[
,则问题转化为h(x)≥0对任意x∈[![]() ,+∞)恒成立,对m分情况,对h(x)求导研究函数的单调性,得到函数最小值,最小值大于等于0即可.
,+∞)恒成立,对m分情况,对h(x)求导研究函数的单调性,得到函数最小值,最小值大于等于0即可.
(1)![]() ,
,![]() ,
,
因为函数f(x)的图象在点(3,f(3))处的切线与函数g(x)的图象在点(1,g(1))处的切线平行,
所以f'(3)=g'(1).
所以![]() ,化简得
,化简得![]() .
.
(2)由(1)得,![]() ,
,
若b=a,则![]() ,解得a=2或
,解得a=2或![]() (舍去,因为a>0).
(舍去,因为a>0).
所以a=b=2.
所以f(x)=ln(2+2x),![]() .
.
令2+2x>0,得x>-1,则函数f(x)=ln(2+2x)的定义域是(-1,+∞);
令1+x≠0,得x≠-1,则函数![]() 的定义域是(-∞,-1)∪(-1,+∞).
的定义域是(-∞,-1)∪(-1,+∞).
f(x)≥mg(x)对任意x∈[![]() ,+∞)恒成立,即
,+∞)恒成立,即![]() 对任意x∈[
对任意x∈[![]() ,+∞)恒成立.
,+∞)恒成立.
令![]() ,则问题转化为h(x)≥0对任意x∈[
,则问题转化为h(x)≥0对任意x∈[![]() ,+∞)恒成立.
,+∞)恒成立.
![]() .
.
①当![]() ,即x+1-m≥0时,h'(x)≥0且h'(x)不恒为0,
,即x+1-m≥0时,h'(x)≥0且h'(x)不恒为0,
所以函数![]() 在区间[
在区间[![]() ,+∞)上单调递增.
,+∞)上单调递增.
又![]() ,
,
所以h(x)≥0对任意x∈[![]() ,+∞)恒成立.故
,+∞)恒成立.故![]() 符合题意.
符合题意.
②当![]() 时,令
时,令![]() ,得
,得![]() ;
;
令![]() ,得x>m-1.
,得x>m-1.
所以函数![]() 在区间[
在区间[![]() ,m-1)上单调递减,在区间(m-1,+∞)上单调递增,
,m-1)上单调递减,在区间(m-1,+∞)上单调递增,
所以![]() .即当
.即当![]() 时,存在
时,存在![]() ,使h(x0)<0.
,使h(x0)<0.
故知h(x)≥0对任意x∈[![]() ,+∞)不恒成立.故
,+∞)不恒成立.故![]() 不符合题意.
不符合题意.
综上可知,实数m的取值范围是(-∞,![]() ].
].

 53随堂测系列答案
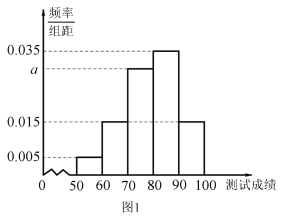
53随堂测系列答案【题目】顺义区教委对本区高一,高二年级学生体质健康测试成绩进行抽样分析.学生测试成绩满分为100分,90分及以上为优秀,60分以下为不及格.先从两个年级各抽取100名学生的测试成绩.其中高一年级学生测试成绩统计结果如图1,高二年级学生测试成绩统计结果如表1.
分组 | 人数 |
|
|
|
|
|
|
|
|
|
|
表1
(1)求图1中a的值;
(2)为了调查测试成绩不及格的同学的具体情况,决定从样本中不及格的学生中抽取3人,用X表示抽取的3人中高二年级的学生人数.求X的分布列及均值;
(3)若用以上抽样数据估计全区学生体质健康情况.用Y表示从全区高二年级全部学生中任取3人中成绩优秀的人数,求EY的值;
(4)用![]() ,
,![]() ,分别表示样本中高一,高二年级学生测试成绩的方差,比较其大小(只需写出结果).
,分别表示样本中高一,高二年级学生测试成绩的方差,比较其大小(只需写出结果).
【题目】王明、李东、张红三位同学在第一、第二学期消费的部分文具的数量如表所示:
姓名 | 第一学期 | 第二学期 | ||||||
笔记本 | 练习本 | 水笔 | 铅笔 | 笔记本 | 练习本 | 水笔 | 铅笔 | |
王明 | 3 | 5 | 2 | 4 | 4 | 6 | 3 | 3 |
李东 | 2 | 6 | 3 | 3 | 4 | 8 | 5 | 2 |
张红 | 4 | 7 | 4 | 2 | 5 | 10 | 6 | 4 |
若笔记本的单价为每本5元;练习本每本2元;水笔每支3元;铅笔每支1元.求三位学生在这些文具上各自花费的金额.
【题目】某中学为了解中学生的课外阅读时间,决定在该中学的1200名男生和800名女生中按分层抽样的方法抽取20名学生,对他们的课外阅读时间进行问卷调查。现在按课外阅读时间的情况将学生分成三类:A类(不参加课外阅读),B类(参加课外阅读,但平均每周参加课外阅读的时间不超过3小时),C类(参加课外阅读,且平均每周参加课外阅读的时间超过3小时)。调查结果如下表:
A类 | B类 | C类 | |
男生 | x | 5 | 3 |
女生 | y | 3 | 3 |
(I)求出表中x,y的值;
(II)根据表中的统计数据,完成下面的列联表,并判断是否有90%的把握认为“参加课外阅读与否”与性别有关;
男生 | 女生 | 总计 | |
不参加课外阅读 | |||
参加课外阅读 | |||
总计 |
(III)从抽出的女生中再随机抽取3人进一步了解情况,记X为抽取的这3名女生中A类人数和C类人数差的绝对值,求X的数学期望。
附:K2=![]() )
)
P(K2≥k0) | 0.10 | 0.01 | |
k0 | 2.706 | 3.841 | 6.635 |
【题目】某市为了了解民众对开展创建文明城市工作以来的满意度,随机调查了40名群众,并将他们随机分成A,B两组,每组20人,A组群众给第一阶段的创文工作评分,B组群众给第二阶段的创文工作评分,根据两组群众的评分绘制了如下茎叶图:
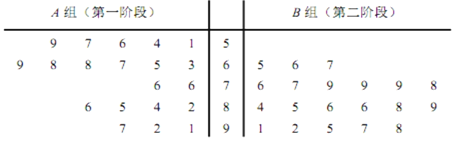
![]() 根据茎叶图比较群众对两个阶段创文工作满意度评分的平均值及集中程度
根据茎叶图比较群众对两个阶段创文工作满意度评分的平均值及集中程度![]() 不要求计算出具体值,给出结论即可
不要求计算出具体值,给出结论即可![]() ;
;
![]() 根据群众的评分将满意度从低到高分为三个等级:
根据群众的评分将满意度从低到高分为三个等级:
满意度评分 | 低于70分 | 70分到89分 | 不低于90分 |
满意度等级 | 不满意 | 满意 | 非常满意 |
![]() 假设两组群众的评价结果相互独立,由频率估计概率,求创文工作第二阶段的民众满意度等级高于第一阶段的概率;
假设两组群众的评价结果相互独立,由频率估计概率,求创文工作第二阶段的民众满意度等级高于第一阶段的概率;
![]() 从这40名群众中随机抽取2人,记X表示满意度等级为“非常满意”的群众人数,求X的分布列与数学期望.
从这40名群众中随机抽取2人,记X表示满意度等级为“非常满意”的群众人数,求X的分布列与数学期望.