Question

【题目】某市为了了解民众对开展创建文明城市工作以来的满意度，随机调查了40名群众，并将他们随机分成A，B两组，每组20人，A组群众给第一阶段的创文工作评分，B组群众给第二阶段的创文工作评分，根据两组群众的评分绘制了如下茎叶图：

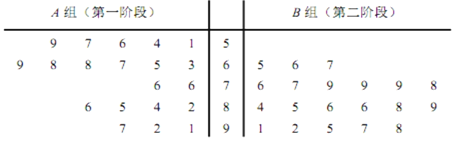
根据茎叶图比较群众对两个阶段创文工作满意度评分的平均值及集中程度不要求计算出具体值，给出结论即可；

根据群众的评分将满意度从低到高分为三个等级：

满意度评分	低于70分	70分到89分	不低于90分
满意度等级	不满意	满意	非常满意

假设两组群众的评价结果相互独立，由频率估计概率，求创文工作第二阶段的民众满意度等级高于第一阶段的概率；

从这40名群众中随机抽取2人，记X表示满意度等级为“非常满意”的群众人数，求X的分布列与数学期望．

Answer 1

【答案】（1）见解析；（2）； 见解析.

【解析】

通过茎叶图可以看出：B组群众给第二阶段创文工作满意度评分相对集中在峰值的随近，由此得到B组级第二阶段创文工作满意度评分的平均分高于A组群众给第一阶段创文工作满意度评分的平均值，给分相对A组更集中稳定．

记表示事件“第一阶段创文工作满意度等级为不满意”，表示事件“第一阶段创文工作满意度等级为满意”，表示事件“第二阶段创文工作满意度等级为满意或非常满意”，表示事件“第二阶段创文工作满意度等级为非常满意”，则由频率估计概率，得：，，，，设创文工作第二阶段的民众满意度等级高于第一阶段为事件A，由事件的相互独立性，能求出创文工作第二阶段的民众满意度等级高于第一阶段的概率由已知在被随机调查的40名群众中，创文工作满意度为“非常满意”的人数为8人，其他等级为32人，则从中随机抽取2人，，1，2，分别求出相应的概率，由此能求出X的分布列和．

通过茎叶图可以看出：B组群众给第二阶段创文工作满意度评分的“叶”分布在“茎”的7，8，9上，也相对集中在峰值的随近，

故B组级第二阶段创文工作满意度评分的平均分高于A组群众给第一阶段创文工作满意度评分的平均值，

给分相对A组更集中稳定．

记表示事件“第一阶段创文工作满意度等级为不满意”，

表示事件“第一阶段创文工作满意度等级为满意”，

表示事件“第二阶段创文工作满意度等级为满意或非常满意”，

表示事件“第二阶段创文工作满意度等级为非常满意”，

则由频率估计概率，得：，，，，

设创文工作第二阶段的民众满意度等级高于第一阶段为事件A，

由事件的相互独立性，得创文工作第二阶段的民众满意度等级高于第一阶段的概率：

．

由已知在被随机调查的40名群众中，创文工作满意度为“非常满意”的人数为8人，

其他等级为32人，则从中随机抽取2人，，1，2，

，

，

，

的分布列为：

X	0	1	2
P

．