Question

【题目】已知圆A：（x+1）2+y2＝16，圆C过点B（1，0）且与圆A相切，设圆心C的轨迹为曲线E．

（Ⅰ）求曲线E的方程；

（Ⅱ）过点B作两条互相垂直的直线l1，l2，直线l1与E交于M，N两点，直线l2与圆A交于P，Q两点，求的取值范围．

Answer 1

【答案】（I）；（II）.

【解析】

（Ⅰ）由题意画出图形，根据椭圆的定义和性质求出a，b，则椭圆方程可求；

（Ⅱ）求出两直线垂直于坐标轴时的值，当两直线斜率存在且不为0时，设l1：y＝k（x﹣1），则l2：y，分别求出|MN|，|PQ|的值，可得关于k的函数，利用配方法求值域．

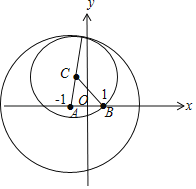
（Ⅰ）圆A：（x+1）2+y2＝16的圆心A（﹣1，0），半径r＝4，如图，

由图可知，|CA|+|CB|＝r＝4，

∴圆心C的轨迹为以A，B为焦点的椭圆，且c＝1，2a＝4，a＝2．

∴b．

则曲线E的方程为；

（Ⅱ）如图，当l1⊥x轴，l2⊥y轴时，；

当l1⊥y轴，l2⊥x轴时，；

当两直线斜率存在且不为0时，设l1：y＝k（x﹣1），

则l2：y．

联立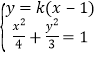，得（3+4k2）x2﹣8k2x+4k2﹣12＝0．

设M（x1，y1），N（x2，y2），

则，，

∴|MN||x1﹣x2|

．

圆心A到直线x+ky﹣1＝0的距离d，

则|PQ|＝2．

∴．

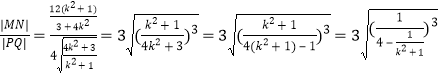∵k2+1＞1，∴，则，

∴∈（），

综上，的取值范围为[]．