题目内容
【题目】已知函数![]() (a>0).
(a>0).
(1)讨论函数f(x)的单调性;
(2)证明:对任意x∈[1,+∞),有f(x)≤2x-a2.
【答案】(1)详见解析(2)详见解析
【解析】
(1)对函数求导,分情况讨论导函数的正负,进而得到单调区间;(2)构造函数![]() ,对函数求导,研究函数的单调性,得到函数的最值,证明函数的最大值小于0即可.
,对函数求导,研究函数的单调性,得到函数的最值,证明函数的最大值小于0即可.
(1)解: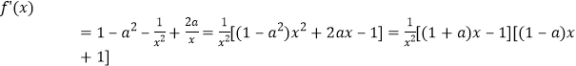 .
.
①当0<a≤1时,由f'(x)<0,得[(1+a)x-1][(1-a)x+1]<0,
解得![]() ;
;
由f'(x)>0,得[(1+a)x-1][(1-a)x+1]>0,解得![]() .
.
故函数f(x)的单调递减区间为(0,![]() ),单调递增区间为(
),单调递增区间为(![]() ,+∞).
,+∞).
②当a>1时,由f'(x)<0,得![]() 或
或![]() ;
;
由f'(x)>0,得![]() .
.
故函数f(x)的单调递减区间为(0,![]() ),(
),(![]() ,+∞),单调递增区间为
,+∞),单调递增区间为![]() .
.
(2)证明:构造函数![]() ,
,
则![]() .
.
因为Δ=(2a)2-4(1+a2)<0,
所以(1+a2)x2-2ax+1>0,即g'(x)<0.
故g(x)在区间[1,+∞)上是减函数.
又x≥1,所以g(x)≤g(1)=-(1+a2)+1+a2=0.
故对任意x∈[1,+∞),有f(x)≤2x-a2.

 口算题天天练系列答案
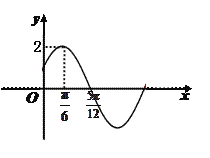
口算题天天练系列答案【题目】某同学用“五点法”画函数![]() 在某一个周期内的图象时,列表并填入了部分数据,如下表:
在某一个周期内的图象时,列表并填入了部分数据,如下表:
| 0 |
|
|
|
|
|
|
| |||
| 0 | 2 | 0 | 0 |
(1)请将上表数据补充完整,填写在相应位置,并求出函数![]() 的解析式;
的解析式;
(2)把![]() 的图象上所有点的横坐标伸长到原来的2倍(纵坐标不变),再把得到的图象向左平移
的图象上所有点的横坐标伸长到原来的2倍(纵坐标不变),再把得到的图象向左平移![]() 个单位长度,得到函数
个单位长度,得到函数![]() 的图象,求
的图象,求![]() 的值.
的值.
【题目】假设关于某种设备的使用年限![]() (年)与所支出的维修费用
(年)与所支出的维修费用![]() (万元)有如下统计:
(万元)有如下统计:
| 2 | 3 | 4 | 5 | 6 |
| 2.2 | 3.8 | 5.5 | 6.5 | 7.0 |
已知![]() ,
, ![]() .
. 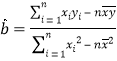 ,
, ![]()
(1)求![]() ,
, ![]() ;
;
(2)![]() 与
与![]() 具有线性相关关系,求出线性回归方程;
具有线性相关关系,求出线性回归方程;
(3)估计使用年限为10年时,维修费用约是多少?