题目内容
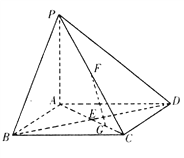
【题目】如图,在长方体ABCD﹣A1B1C1D1中,A1C1与B1D1的交点为O1 , AC与BD的交点为O.
(1)求证:直线OO1∥平面BCC1B1;
(2)若AB=BC,求证:直线BO⊥平面ACC1A1 .
【答案】
(1)证明:在长方体ABCD﹣A1B1C1D1中,A1C1与B1D1的交点为O1,O1是A1C1的中点.
AC与BD的交点为O.O是AC的中点.
ACC1A1是矩形,可知OO1∥CC1,CC1平面BCC1B1,
OO1平面BCC1B1,
∴直线OO1∥平面BCC1B1

(2)证明:AB=BC,所以△ABC是等腰三角形,BO⊥AC,AA1⊥BO,AA1∩AC=A,
∴直线BO⊥平面ACC1A1.
【解析】第(1)问应用线面平行的判定定理即可。
第(2)问要正面线面垂直,关键是线垂直于面内两条线,因此只要证明BO⊥AC,AA1⊥BO即可;
【考点精析】根据题目的已知条件,利用直线与平面平行的判定和直线与平面垂直的判定的相关知识可以得到问题的答案,需要掌握平面外一条直线与此平面内的一条直线平行,则该直线与此平面平行;简记为:线线平行,则线面平行;一条直线与一个平面内的两条相交直线都垂直,则该直线与此平面垂直;注意点:a)定理中的“两条相交直线”这一条件不可忽视;b)定理体现了“直线与平面垂直”与“直线与直线垂直”互相转化的数学思想.

【题目】在![]() 年初的时候,国家政府工作报告明确提出,
年初的时候,国家政府工作报告明确提出, ![]() 年要坚决打好蓝天保卫战,加快解决燃煤污染问题,全面实施散煤综合治理.实施煤改电工程后,某县城的近六个月的月用煤量逐渐减少,
年要坚决打好蓝天保卫战,加快解决燃煤污染问题,全面实施散煤综合治理.实施煤改电工程后,某县城的近六个月的月用煤量逐渐减少, ![]() 月至
月至![]() 月的用煤量如下表所示:
月的用煤量如下表所示:
月份 |
|
|
|
|
|
|
用煤量 |
|
|
|
|
|
|
(1)由于某些原因, ![]() 中一个数据丢失,但根据
中一个数据丢失,但根据![]() 至
至![]() 月份的数据得出
月份的数据得出![]() 样本平均值是
样本平均值是![]() ,求出丢失的数据;
,求出丢失的数据;
(2)请根据![]() 至
至![]() 月份的数据,求出
月份的数据,求出![]() 关于
关于![]() 的线性回归方程
的线性回归方程![]() ;
;
(3)现在用(2)中得到的线性回归方程中得到的估计数据与![]() 月
月![]() 月的实际数据的误差来判断该地区的改造项目是否达到预期,若误差均不超过
月的实际数据的误差来判断该地区的改造项目是否达到预期,若误差均不超过![]() ,则认为该地区的改造已经达到预期,否则认为改造未达预期,请判断该地区的煤改电项目是否达预期?
,则认为该地区的改造已经达到预期,否则认为改造未达预期,请判断该地区的煤改电项目是否达预期?
(参考公式:线性回归方程![]() ,其中
,其中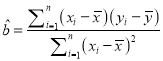
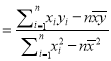 )
)