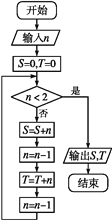
题目内容
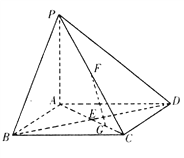
【题目】如图,在底面是正方形的四棱锥![]() 面ABCD,BD交AC于点E,F是PC中点,G为AC上一点.
面ABCD,BD交AC于点E,F是PC中点,G为AC上一点.
(1)求证:![]() ;
;
(2)确定点G在线段AC上的位置,使FG//平面PBD,并说明理由;
(3)当二面角![]() 的大小为
的大小为![]() 时,求PC与底面ABCD所成角的正切值.
时,求PC与底面ABCD所成角的正切值.
【答案】(1)见解析(2)G为EC中点(3)![]()
【解析】试题分析:(1)要证:BD⊥FG,先证BD⊥平面PAC即可;(2)确定点G在线段AC上的位置,使FG∥平面PBD,FG∥平面PBD内的一条直线即可;(3)利用向量数量积求解法向量,然后转化求出PC与底面ABCD所成角的正切值.
解析:
(1)![]()
![]()
![]()
![]()
(2)当G为EC中点,即![]() 时, FG//平面PBD
时, FG//平面PBD
理由如下:
连接PE,![]() F为PC中点,G为EC中点,
F为PC中点,G为EC中点,![]() FG//PE
FG//PE
![]()
![]() FG//平面PBD
FG//平面PBD

(3)作![]() 作于H,连接DH,
作于H,连接DH,![]() ,四边形ABCD是正方形,
,四边形ABCD是正方形,![]()
又![]()
![]()
![]() 是二面角的平面角,即
是二面角的平面角,即![]()
![]()
![]() 是PC与底面ABCD所成角
是PC与底面ABCD所成角
连接EH,则![]()
![]()
又![]()
![]()
![]()
![]() ,
, ![]()
![]() PC与与底面ABCD所成角的正切值是
PC与与底面ABCD所成角的正切值是![]() .
.

【题目】某研究所计划利用“神十”宇宙飞船进行新产品搭载实验,计划搭载若干件新产品A、B,该所要根据该产品的研制成本、产品重量、搭载实验费用和预计产生的收益来决定具体搭载安排,有关数据如表:
每件产品A | 每件产品B | ||
研制成本、搭载 | 20 | 30 | 计划最大资金额 |
产品重量(千克) | 10 | 5 | 最大搭载重量110千克 |
预计收益(万元) | 80 | 60 |
分别用x,y表示搭载新产品A,B的件数.总收益用Z表示
(Ⅰ)用x,y列出满足生产条件的数学关系式,并画出相应的平面区域;
(Ⅱ)问分别搭载新产品A、B各多少件,才能使总预计收益达到最大?并求出此最大收益.
【题目】某校为评估新教改对教学的影响,挑选了水平相当的两个平行班进行对比试验.甲班采用创新教法,乙班仍采用传统教法,一段时间后进行水平测试,成绩结果全部落在[60,100]区间内(满分100分),并绘制频率分布直方图如图,两个班人数均为60人,成绩80分及以上为优良. 
(1)根据以上信息填好下列2×2联表,并判断出有多大的把握认为学生成绩优良与班级有关?
是否优良 | 优良(人数) | 非优良(人数) | 合计 |
甲 | |||
乙 | |||
合计 |
(2)以班级分层抽样,抽取成绩优良的5人参加座谈,现从5人中随机选2人来作书面发言,求2人都来自甲班的概率. 下面的临界值表供参考:
P(x2k) | 0.10 | 0.05 | 0.010 |
k | 2.706 | 3.841 | 6.635 |
(以下临界值及公式仅供参考 ![]() ,n=a+b+c+d)
,n=a+b+c+d)