题目内容
已知函数 若函数
若函数 的图像有三个不同的交点,求实数a的取值范围。
的图像有三个不同的交点,求实数a的取值范围。
 若函数
若函数 的图像有三个不同的交点,求实数a的取值范围。
的图像有三个不同的交点,求实数a的取值范围。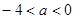
本试题主要是研究函数图像与图像 的交点问题的运用。根据已知中函数图像的关系可知,转换为方程根的问题来处理,即为关于x的方程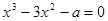 有三个不同的实数根
有三个不同的实数根
然后构造函数借助于导数的极值来判定结论。
解:函数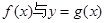 的图像有三个不同的交点等价于方程
的图像有三个不同的交点等价于方程
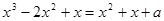 有三个不同的实数根。即关于x的方程
有三个不同的实数根。即关于x的方程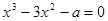 有三个不同的实数根。令
有三个不同的实数根。令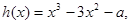 则
则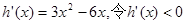 ,解得
,解得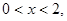 令
令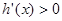 ,解得
,解得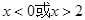 。所以
。所以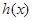 在
在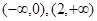 上为增函数,在(0,2)上为减函数。所以
上为增函数,在(0,2)上为减函数。所以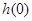 为极大值,h(2)为极小值。从而
为极大值,h(2)为极小值。从而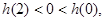 解得
解得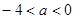
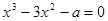 有三个不同的实数根
有三个不同的实数根然后构造函数借助于导数的极值来判定结论。
解:函数
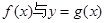 的图像有三个不同的交点等价于方程
的图像有三个不同的交点等价于方程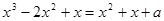 有三个不同的实数根。即关于x的方程
有三个不同的实数根。即关于x的方程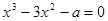 有三个不同的实数根。令
有三个不同的实数根。令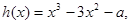 则
则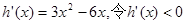 ,解得
,解得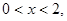 令
令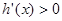 ,解得
,解得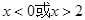 。所以
。所以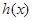 在
在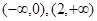 上为增函数,在(0,2)上为减函数。所以
上为增函数,在(0,2)上为减函数。所以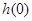 为极大值,h(2)为极小值。从而
为极大值,h(2)为极小值。从而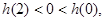 解得
解得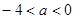

练习册系列答案
 发散思维新课堂系列答案
发散思维新课堂系列答案
相关题目
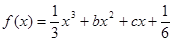 的图象在点
的图象在点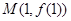 处的切线方程为
处的切线方程为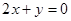 。
。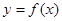 的解析式;
的解析式;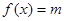 在区间
在区间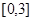 上恰有两个相异实根,求m的取值范围。
上恰有两个相异实根,求m的取值范围。 ,其中a为实数。
,其中a为实数。 的单调区间;
的单调区间; 对定义域内的任意x恒成立,求实数a的取值范围。
对定义域内的任意x恒成立,求实数a的取值范围。 恒成立。
恒成立。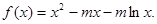
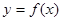 在点(1,
在点(1,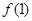 )处的切线与x轴平行.
)处的切线与x轴平行.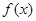 的最值;
的最值;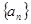 满足
满足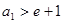 (
(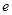 为自然对数的底数),
为自然对数的底数),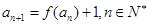 ,
,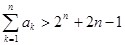 .
.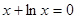 的实根为
的实根为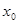 .
.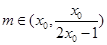 ,存在
,存在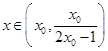 使
使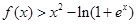 成立.
成立.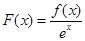 是定义在R上的函数,其中
是定义在R上的函数,其中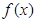 的导函数为
的导函数为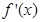 ,满足
,满足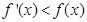 对于
对于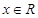 恒成立,则( )
恒成立,则( )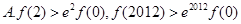


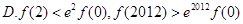
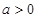 ,函数
,函数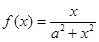 的导函数为
的导函数为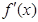 .
.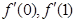 的值,并比较它们的大小;
的值,并比较它们的大小;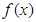 的极值.
的极值.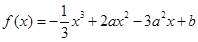 (常数a,b满足0<a<1,b
(常数a,b满足0<a<1,b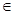 R)
R)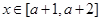 ,不等式|
,不等式| a恒成立,求a的取值范围。
a恒成立,求a的取值范围。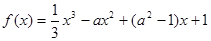 的极小值点在(0,1)内,则实数
的极小值点在(0,1)内,则实数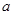 的取值范围是( )
的取值范围是( ) ,-1)上为增函数,在(-1,1)上为减函数,则f(1)为( )
,-1)上为增函数,在(-1,1)上为减函数,则f(1)为( )