题目内容
设函数 (常数a,b满足0<a<1,b
(常数a,b满足0<a<1,b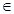 R)
R)
(1)求函数f(x)的单调区间和极值;
(2)若对任意的 ,不等式|
,不等式|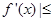 a恒成立,求a的取值范围。
a恒成立,求a的取值范围。
 (常数a,b满足0<a<1,b
(常数a,b满足0<a<1,b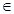 R)
R)(1)求函数f(x)的单调区间和极值;
(2)若对任意的
 ,不等式|
,不等式|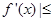 a恒成立,求a的取值范围。
a恒成立,求a的取值范围。(1)f(x)的单调递增区间为(a, 3a),减区间为(-∞,a)和 (3a,+∞)
(2)
(2)

解 (1)f′(x)=-x2+4ax-3a2,令f′(x)>0,
得f(x)的单调递增区间为(a, 3a).
令f′(x)<0,得f(x)的单调递减区间为(-∞,a)和 (3a,+∞),
∴当x=a时,f(x)极小值=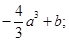
当x=3a时,f(x)极大值="b."
(2)由|f′(x)|≤a,得-a≤-x2+4ax-3a2≤a.∵0<a<1,∴a+1>2a.
∴f′(x)=-x2+4ax-3a2在[a+1,a+2]上是减函数.∴f′(x)max=f′(a+1)=2a-1.
f′(x)min=f(a+2)=4a-4.于是,对任意x∈[a+1,a+2],不等式①恒成立,
等价于 解得
解得
又0<a<1,∴
得f(x)的单调递增区间为(a, 3a).
令f′(x)<0,得f(x)的单调递减区间为(-∞,a)和 (3a,+∞),
∴当x=a时,f(x)极小值=
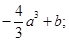
当x=3a时,f(x)极大值="b."
(2)由|f′(x)|≤a,得-a≤-x2+4ax-3a2≤a.∵0<a<1,∴a+1>2a.
∴f′(x)=-x2+4ax-3a2在[a+1,a+2]上是减函数.∴f′(x)max=f′(a+1)=2a-1.
f′(x)min=f(a+2)=4a-4.于是,对任意x∈[a+1,a+2],不等式①恒成立,
等价于
 解得
解得
又0<a<1,∴


练习册系列答案
相关题目
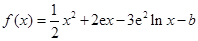 在
在 处的切线斜率为零.
处的切线斜率为零. 和
和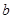 的值;
的值; 恒成立;
恒成立;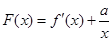 有最小值
有最小值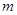 ,且
,且 ,求实数
,求实数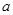 的取值范围.
的取值范围.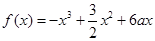 .
.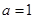 时,求
时,求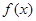 在区间
在区间 上的最值;
上的最值;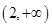 上存在单调递增区间,求
上存在单调递增区间,求 的取值范围.
的取值范围.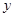 =
=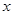 +
+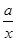 有如下性质:如果常数
有如下性质:如果常数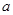 >0,那么该函数在
>0,那么该函数在 0,
0,
 上是减函数,在
上是减函数,在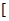
 上是增函数.
上是增函数. (
(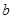 的值;
的值; +
+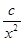 (常数
(常数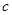 >0)在定义域内的单调性,并说明理由;
>0)在定义域内的单调性,并说明理由;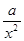 (常数
(常数 (
(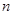 是正整数)在区间[
是正整数)在区间[ ,2]上的最大值和最小值(可利用你的研究结论).
,2]上的最大值和最小值(可利用你的研究结论).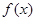 满足
满足 ,当
,当 时有
时有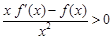 ,则不等式
,则不等式 的解集为( )
的解集为( )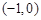
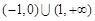


 在
在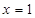 处有极值
处有极值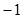 。
。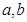 的值;
的值;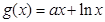 的单调区间。
的单调区间。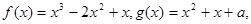 若函数
若函数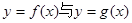 的图像有三个不同的交点,求实数a的取值范围。
的图像有三个不同的交点,求实数a的取值范围。 的两焦点与短轴的一个端点连结成等腰直角三角形,直线
的两焦点与短轴的一个端点连结成等腰直角三角形,直线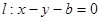 是抛物线
是抛物线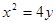 的一条切线。
的一条切线。 交椭圆
交椭圆 于A、B两点,若点P满足
于A、B两点,若点P满足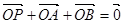 (O为坐标原点), 判断点P是否在椭圆
(O为坐标原点), 判断点P是否在椭圆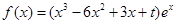 ,
,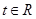 .
.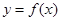 依次在
依次在 处取到极值.
处取到极值.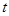 的取值范围;
的取值范围;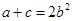 ,求
,求 ,使对任意的
,使对任意的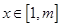 ,不等式
,不等式 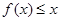 恒成立.求正整数
恒成立.求正整数 的最大值
的最大值