Question

【题目】在平面直角坐标系xOy中，已知抛物线x2=2py（p＞0）上的点M（m，1）到焦点F的距离为2，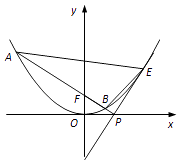
（1）求抛物线的方程；
（2）如图，点E是抛物线上异于原点的点，抛物线在点E处的切线与x轴相交于点P，直线PF与抛物线相交于A，B两点，求△EAB面积的最小值．

Answer 1

【答案】
（1）解：抛物线x2=2py（p＞0）的准线方程为 ，

因为M（m，1），由抛物线定义，知 ，

所以 ，即p=2，

所以抛物线的方程为x2=4y

（2）解：因为 ，所以 ．

设点 ，则抛物线在点E处的切线方程为 ．

令y=0，则 ，即点 ．

因为 ，F（0，1），所以直线PF的方程为 ，即2x+ty﹣t=0．

则点 到直线PF的距离为 ．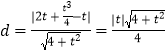

联立方程 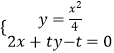消元，得t2y2﹣（2t2+16）y+t2=0．

因为△=（2t2+16）2﹣4t4=64（t2+4）＞0，

所以 ， ，

所以 ．

所以△EAB的面积为 ．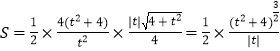

不妨设 （x＞0），则 ．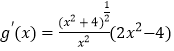

因为 时，g'（x）＜0，所以g（x）在 上单调递减； 上，g'（x）＞0，所以g（x）在 上单调递增．

所以当 时， ．

所以△EAB的面积的最小值为 ．

【解析】（1）求出抛物线x2=2py（p＞0）的准线方程为 ，由抛物线定义，得到p=2，即可求解抛物线的方程．（2）求出函数的 ．设点 ，得到抛物线在点E处的切线方程为 ．求出 ．推出直线PF的方程，点 到直线PF的距离，联立 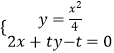求出AB，表示出△EAB的面积，构造函数，通过函数的导数利用单调性求解最值即可．