题目内容
20.已知角θ的顶点为坐标原点O,始边为x轴的非负半轴,且满足sin$\frac{θ}{2}$=$-\frac{3}{5}$,cos$\frac{θ}{2}$=$\frac{4}{5}$,设B为角θ终边上任意一点,$\overrightarrow{OA}=(0,-1)$,则|$\overrightarrow{OA}-\overrightarrow{OB}$|的取值范围是( )| A. | [$\frac{7}{25},+∞)$ | B. | [$\frac{1}{3}$,+∞) | C. | [$\frac{4}{5}$,+∞) | D. | [1,+∞) |
分析 根据向量的三角形法则以及所求的几何意义进行解答.
解答 解:由sin$\frac{θ}{2}$=$-\frac{3}{5}$,cos$\frac{θ}{2}$=$\frac{4}{5}$,得到sinθ=$-\frac{24}{25}$,cosθ=$±\frac{7}{25}$,B为角θ终边上任意一点,$\overrightarrow{OA}=(0,-1)$,则|$\overrightarrow{OA}-\overrightarrow{OB}$|=|$\overrightarrow{BA}$|,设A到OB的距离为b,则$\frac{b}{OA}=\frac{7}{25}$,所以b=$\frac{7}{25}$,
所以|$\overrightarrow{OA}-\overrightarrow{OB}$|的取值范围是[$\frac{7}{25},+∞$);
故选A.
点评 本题考查了正弦的二倍角公式以及向量的三角形法则的几何意义.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
12.若复数z满足(3-4i)z=|4+3i|,则z的虚部为( )
| A. | $\frac{4}{5}$ | B. | -$\frac{4}{5}$i | C. | $\frac{4}{5}$i | D. | 4 |
10.i为虚数单位,(1+i)$\overline{z}$=(1-i)2,则|z|=( )
| A. | 1 | B. | 2 | C. | $\sqrt{2}$ | D. | $2\sqrt{2}$ |
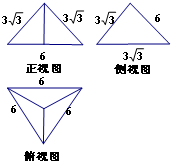 正四面体(即各条棱长均相等的三棱锥)的棱长为6,某学生画出该正四面体的三视图如下,其中有一个视图是错误的,则该视图修改正确后对应图形的面积为6$\sqrt{6}$.该正四面体的体积为18$\sqrt{2}$.
正四面体(即各条棱长均相等的三棱锥)的棱长为6,某学生画出该正四面体的三视图如下,其中有一个视图是错误的,则该视图修改正确后对应图形的面积为6$\sqrt{6}$.该正四面体的体积为18$\sqrt{2}$.