Question

5．已知椭圆C：$\frac{{x}^{2}}{{a}^{2}}+\frac{{y}^{2}}{{b}^{2}}=1（a＞b＞0）$的离心率为$\frac{\sqrt{2}}{2}$，点Q（$\frac{\sqrt{2}}{2}，\frac{\sqrt{3}}{2}$）在椭圆C上．
（Ⅰ）求椭圆C的方程；
（Ⅱ）设P为椭圆C上异于其顶点的动点，O为坐标原点，过椭圆右焦点F₂作OP平行线交椭圆C于A、B两点．
（i）试探究|OP|²和|AB|的比值是否为一个常数？若是，求出这个常数，若不是，请说明理由．
（ii）记△PF₂A的面积为S₁，△OF₂B的面积为S₂，令S=S₁+S₂，求证：S$＜\frac{\sqrt{2}}{2}$．

Answer 1

分析 （Ⅰ）由$\frac{c}{a}=\frac{\sqrt{2}}{2}$，得到a²=2b²，再把点的坐标代入椭圆方程得另一方程，联立方程组求得a，b，则椭圆方程可求；
（Ⅱ）（i）设P（x₀，y₀）（-1＜y₀＜1且y₀≠0），则${{x}_{0}}^{2}+2{{y}_{0}}^{2}=2$，求出OP的斜率，得到AB的斜率，进一步得到AB的方程，和椭圆方程联立，由弦长公式求得AB的长度，结合P在椭圆上整体运算求得$\frac{|OP{|}^{2}}{|AB|}=\frac{{{x}_{0}}^{2}+{{y}_{0}}^{2}}{\sqrt{2}（2-{{y}_{0}}^{2}）}$=$\frac{2-{{y}_{0}}^{2}}{\sqrt{2}（2-{{y}_{0}}^{2}）}=\frac{\sqrt{2}}{2}$；
（ii）画图可得${S}_{△O{F}_{2}B}={S}_{△P{F}_{2}B}$，从而有S=S₁+S₂ =S_△PAB，求出P到AB的距离，结合（i）求得的AB的长度，代入三角形面积公式即可证得答案．

解答 （Ⅰ）解：由题意知$\frac{c}{a}=\frac{\sqrt{2}}{2}$，即$\frac{{c}^{2}}{{a}^{2}}=\frac{1}{2}$，$\frac{{a}^{2}-{b}^{2}}{{a}^{2}}=\frac{1}{2}$，a²=2b²，①
又点Q（$\frac{\sqrt{2}}{2}，\frac{\sqrt{3}}{2}$）在椭圆C上，∴$\frac{1}{2{a}^{2}}+\frac{3}{4{b}^{2}}=1$，②
联立①②，解得a²=2，b²=1．
∴椭圆C的方程为$\frac{{x}^{2}}{2}+{y}^{2}=1$；
（Ⅱ）（i）解：设P（x₀，y₀）（-1＜y₀＜1且y₀≠0），则${{x}_{0}}^{2}+2{{y}_{0}}^{2}=2$，
∴${k}_{OP}=\frac{{y}_{0}}{{x}_{0}}$，则AB所在直线方程为y=$\frac{{y}_{0}}{{x}_{0}}（x-1）$，
联立$\left\{\begin{array}{l}{y=\frac{{y}_{0}}{{x}_{0}}（x-1）}\\{{x}^{2}+2{y}^{2}=2}\end{array}\right.$，得${x}^{2}-2{{y}_{0}}^{2}x+{{y}_{0}}^{2}-{{x}_{0}}^{2}=0$．
设A（x₁，y₁），B（x₂，y₂），
则${x}_{1}+{x}_{2}=2{{y}_{0}}^{2}，{x}_{1}{x}_{2}={{y}_{0}}^{2}-{{x}_{0}}^{2}$，
∴|AB|=$\sqrt{1+\frac{{{y}_{0}}^{2}}{{{x}_{0}}^{2}}}\sqrt{4{{y}_{0}}^{4}-4{{y}_{0}}^{2}+4{{x}_{0}}^{2}}$=$\sqrt{2}（2-{{y}_{0}}^{2}）$．
∴$\frac{|OP{|}^{2}}{|AB|}=\frac{{{x}_{0}}^{2}+{{y}_{0}}^{2}}{\sqrt{2}（2-{{y}_{0}}^{2}）}$=$\frac{2-{{y}_{0}}^{2}}{\sqrt{2}（2-{{y}_{0}}^{2}）}=\frac{\sqrt{2}}{2}$．
∴|OP|²和|AB|的比值是常数$\frac{\sqrt{2}}{2}$；
（ii）证明：如图，
∵OP∥AB，∴${S}_{△O{F}_{2}B}={S}_{△P{F}_{2}B}$，
则S=S₁+S₂ =S_△PAB，
∵|AB|=$\sqrt{2}（2-{{y}_{0}}^{2}）$，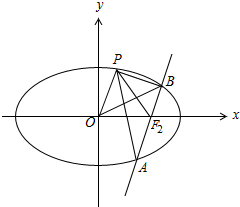
P到直线AB的距离为d=$\frac{|{y}_{0}{x}_{0}-{x}_{0}{y}_{0}-{y}_{0}|}{\sqrt{{{x}_{0}}^{2}+{{y}_{0}}^{2}}}=\frac{|{y}_{0}|}{\sqrt{2-{{y}_{0}}^{2}}}$．
∴$S={S}_{△PAB}=\frac{1}{2}•\sqrt{2}（2-{{y}_{0}}^{2}）•\frac{|{y}_{0}|}{\sqrt{2-{{y}_{0}}^{2}}}$=$\frac{\sqrt{2}}{2}\sqrt{（2-{{y}_{0}}^{2}）•{{y}_{0}}^{2}}=\frac{\sqrt{2}}{2}\sqrt{-{{y}_{0}}^{4}+2{{y}_{0}}^{2}}$
=$\frac{\sqrt{2}}{2}\sqrt{-（{{y}_{0}}^{2}-1）^{2}+1}＜\frac{\sqrt{2}}{2}$．

点评 本题考查椭圆的几何性质，考查了直线和圆锥曲线的位置关系，体现了数学转化思想方法，题目运算量大，考查了学生的运算求解能力，是压轴题．