题目内容
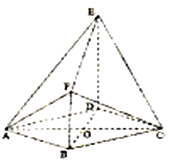
【题目】如图所示，在四棱锥P-ABCD中，底面四边形ABCD是菱形，AC∩BD=O，△PAC是边长为2的等边三角形，
．
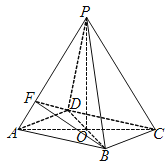
（1）求四棱锥P-ABCD的体积VP-ABCD；
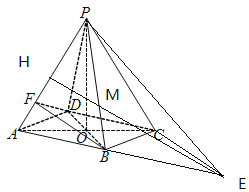
（2）在线段PB上是否存在一点M，使得CM∥平面BDF？如果存在，求
的值，如果不存在，请说明理由．
【答案】（1）2；（2）
【解析】
（1）证明PO⊥平面ABCD，计算PO，AC，BD，代入体积公式计算；
（2）过C构造平面BCE，使得平面BCE∥BDF，利用三角形的中线的性质得出M的位置．
（1）解：∵底面ABCD是菱形，∴O为AC，BD的中点
又∵PA=PC，PB=PD，∴PO⊥AC，PO⊥BD，
∵AC∩BD=O，AC面ABCD，BD面ABCD，
∴PO⊥底面ABCD．
△PAC中，AC=2，∴
，△PBD中，
，
，
．
（2）过C作CE∥BD交AB延长线于E，过E作EH∥BF交PA于H，EH与PB交点为M，
∵CE∥BD，BD面BDF，CE面BDF，∴CE∥面BDF，
∵EH∥BF，BF面BDF，EH面BDF，∴EH∥面BDF，
又∵CE∩EH=E，CE面CEM，EH面CEM，
∴面BDF∥面CEM，CM面CEM，
∴CM∥面BDF，
∵BD∥CE，DC∥BE，
∴四边形BECD为平行四边形，∴DC=BE=AB，B为AE中点，
∵
∴H为PA中点，
∴M为中线PB与中线EH的交点，
∴M是△APE的重心，∴
=．
练习册系列答案
相关题目
