题目内容
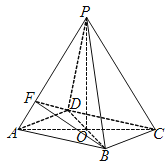
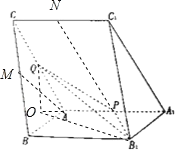
【题目】如图,三棱柱![]() 中,
中,![]() 分别为棱
分别为棱![]() 的中点.
的中点.
(1)在![]() 上确定点M,使
上确定点M,使![]() 平面
平面![]() ,并说明理由。
,并说明理由。
(2)若侧面![]() 侧面
侧面![]() ,求直线
,求直线![]() 与平面
与平面![]() 所成角的正弦值。
所成角的正弦值。
【答案】(1)答案见解析;(2)![]() .
.
【解析】
(1)取BC中点M,连接AM,则AM∥平面PQB1;利用面面平行证明线面平行即可;
(2)作QO⊥平面ABB1A1,与A1A延长线交于O,作PN∥C1A1,则直线A1C1与平面PQB1所成角即直线PN与平面PQB1所成角,结合几何关系求解直线![]() 与平面
与平面![]() 所成角的正弦值即可.
所成角的正弦值即可.
(1)取BC中点M,连接AM,则AM∥平面PQB1;
如图所示,取BB1中点N,连结AM,AN,
![]() 为平行四边形,点N,P为中点,则
为平行四边形,点N,P为中点,则![]() ,由线面平行的判定定理可得
,由线面平行的判定定理可得![]() 平面PQB1,
平面PQB1,
同理可得,![]() 平面PQB1,
平面PQB1,
据此可得平面AMN∥平面PQB1,故![]() 平面
平面![]() .
.
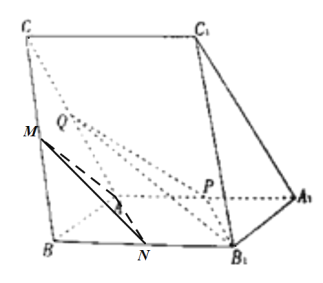
(2)作QO⊥平面ABB1A1,与A1A延长线交于O,
则![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() .
.
作PN∥C1A1,则直线A1C1与平面PQB1所成角即直线PN与平面PQB1所成角,
![]() .
.
设N到平面PQB1的距离为h,则![]() ,
,
∴直线A1C1与平面PQB1所成角的正弦值为:![]() .
.

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案【题目】某地区高考实行新方案,规定:语文、数学和英语是考生的必考科目,考生还须从物理、化学、生物、历史、地理和政治六个科目中选出了三个科目作为选考科目.若一名学生从六个科目中选出了三个科目作为选考科目,则称该学生的选考方案确定;否则,称该学生选考方案待确定.某学校为了了解高一年级200名学生选考科目的意向,随机选取20名学生进行了一次调查,统计选考科目人数如下表:
性别 | 选考方案确定情况 | 物理 | 化学 | 生物 | 历史 | 地理 | 政治 |
男生 | 选考方案确定的有5人 | 5 | 5 | 2 | 1 | 2 | 0 |
选考方案待确定的有7人 | 6 | 4 | 3 | 2 | 4 | 2 | |
女生 | 选考方案确定的有6人 | 3 | 5 | 2 | 3 | 3 | 2 |
选考方案待确定的有2人 | 1 | 2 | 1 | 0 | 1 | 1 |
(1)在选考方案确定的男生中,同时选考物理、化学、生物的人数有多少?
(2)从选考方案确定的男生中任选2名,试求出这2名学生选考科目完全相同的概率.
【题目】某高校在2019年的自主招生笔试成绩(满分200分)中,随机抽取100名考生的成绩,按此成绩分成五组,得到如下的频率分布表:
组号 | 分组 | 频数 | 频率 |
第一组 |
| 15 |
|
第二组 |
| 25 | 0.25 |
第三组 |
| 30 | 0.3 |
第四组 |
|
|
|
第五组 |
| 10 | 0.1 |
(1)求频率分布表中![]() ,
,![]() ,
,![]() 的值;
的值;
(2)估计笔试成绩的平均数及中位数(同一组中的数据用该组区间的中点值作代表);(精确到0.1)
(3)若从第四组、第五组的学生中按组用分层抽样的方法抽取6名学生参加面试,用简单随机抽样方法从6人中抽取2人作为正、副小组长,求“抽取的2人为同一组”的概率.
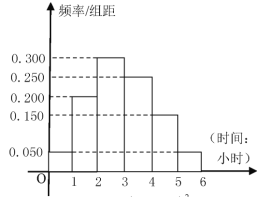
【题目】某校共有学生2000人,其中男生1100人,女生900人为了调查该校学生每周平均课外阅读时间,采用分层抽样的方法收集该校100名学生每周平均课外阅读时间(单位:小时)
(1)应抽查男生与女生各多少人?
(2)如图,根据收集100人的样本数据,得到学生每周平均课外阅读时间的频率分布直方图,其中样本数据分组区间为![]() .若在样本数据中有38名女学生平均每周课外阅读时间超过2小时,请完成每周平均课外阅读时间与性别的列联表,并判断是否有95%的把握认为“该校学生的每周平均课外阅读时间与性别有关”.
.若在样本数据中有38名女学生平均每周课外阅读时间超过2小时,请完成每周平均课外阅读时间与性别的列联表,并判断是否有95%的把握认为“该校学生的每周平均课外阅读时间与性别有关”.
男生 | 女生 | 总计 | |
每周平均课外阅读时间不超过2小时 | |||
每周平均课外阅读时间超过2小时 | |||
总计 |
附:
| 0.100 | 0.050 | 0.010 | 0.005 |
| 2.706 | 3.841 | 6.635 | 7.879 |