题目内容
【题目】如图,椭圆![]() 经过点
经过点![]() ,且点
,且点![]() 到椭圆的两焦点的距离之和为
到椭圆的两焦点的距离之和为![]() .
.
(l)求椭圆![]() 的标准方程;
的标准方程;
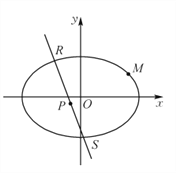
(2)若![]() 是椭圆
是椭圆![]() 上的两个点,线段
上的两个点,线段![]() 的中垂线
的中垂线![]() 的斜率为
的斜率为![]() 且直线
且直线![]() 与
与![]() 交于点
交于点![]() ,
,![]() 为坐标原点,求证:
为坐标原点,求证:![]() 三点共线.
三点共线.
【答案】(1) ![]() (2)见解析
(2)见解析
【解析】分析:
(1)根据椭经过点![]() ,且点
,且点![]() 到椭圆的两焦点的距离之和为
到椭圆的两焦点的距离之和为![]() ,结合性质
,结合性质![]() ,,列出关于
,,列出关于![]() 、
、![]() 的方程组,求出
的方程组,求出![]() 、
、![]() ,即可得椭圆
,即可得椭圆![]() 的标准方程;
的标准方程;
(2)可设直线![]() 的方程为
的方程为![]() ,联立
,联立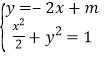 得
得![]() ,设点
,设点![]() ,根据韦达定理可得
,根据韦达定理可得![]() ,所以点
,所以点![]() 在直线
在直线![]() 上,又点
上,又点![]() 也在直线
也在直线![]() 上,进而得结果.
上,进而得结果.
详解:
(1)因为点![]() 到椭圆的两焦点的距离之和为
到椭圆的两焦点的距离之和为![]() ,
,
所以![]() ,解得
,解得![]() .
.
又椭圆![]() 经过点
经过点![]() ,所以
,所以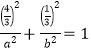 .
.
所以![]() .
.
所以椭圆![]() 的标准方程为
的标准方程为![]() .
.
证明:(2)因为线段![]() 的中垂线
的中垂线![]() 的斜率为
的斜率为![]() ,
,
所以直线![]() 的斜率为-2.
的斜率为-2.
所以可设直线![]() 的方程为
的方程为![]() .
.
据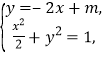 得
得![]() .
.
设点![]() ,
,![]() ,
,![]() .
.
所以![]() ,
,![]()
![]() .
.
所以![]() ,
,![]() .
.
因为![]() ,所以
,所以![]() .
.
所以点![]() 在直线
在直线![]() 上.
上.
又点![]() ,
,![]() 也在直线
也在直线![]() 上,
上,
所以![]() 三点共线.
三点共线.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
【题目】在对人们的休闲方式的一次调查中,共调查了110人,其中女性50人,男性60人.女性中有30人主要的休闲方式是看电视,另外20人主要的休闲方式是运动;男性中有20人主要的休闲方式是看电视,另外40人主要的休闲方式是运动.
(1)根据以上数据建立一个![]() 列联表;
列联表;
(2)判断是否有99%的把握认为性别与休闲方式有关系.
下面临界值表供参考:
| 0.10 | 0.05 | 0.010 | 0.001 |
k | 2.706 | 3.841 | 6.635 | 10.828 |
(参考公式: )
)