题目内容
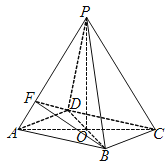
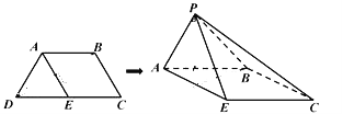
【题目】如图,等腰梯形![]() 中,
中,![]() ,
,![]() ,
,![]() ,
,![]() 为
为![]() 中点,以
中点,以![]() 为折痕把
为折痕把![]() 折起,使点
折起,使点![]() 到达点
到达点![]() 的位置(
的位置(![]() 平面
平面![]() ).
).
(Ⅰ)证明:![]() ;
;
(Ⅱ)若直线![]() 与平面
与平面![]() 所成的角为
所成的角为![]() ,求二面角
,求二面角![]() 的余弦值.
的余弦值.
【答案】(I)见解析;(II)![]() .
.
【解析】
(I)先证明![]() ,再证明
,再证明![]() ;(II)在平面POB内作PQ⊥OB,垂足为Q,
;(II)在平面POB内作PQ⊥OB,垂足为Q,
证明OP⊥平面ABCE,以O为原点,OE为x轴,OB为y轴,OP为z轴,建立空间直角坐标系,利用向量法求二面角![]() 的余弦值.
的余弦值.
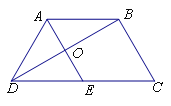
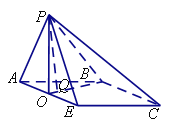
(I)证明:在等腰梯形ABCD中,连接BD,交AE于点O,
∵AB||CE,AB=CE,∴四边形ABCE为平行四边形,∴AE=BC=AD=DE,
∴△ADE为等边三角形,∴在等腰梯形ABCD中,![]() ,
,![]() ,
,
∴在等腰![]() 中,
中,![]()
∴![]() ,即BD⊥BC,
,即BD⊥BC,
∴BD⊥AE,
翻折后可得:OP⊥AE,OB⊥AE,又![]() ,
,![]() ,
,
![]() ;
;
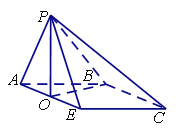
(II)解:在平面POB内作PQ⊥OB,垂足为Q,
因为AE⊥平面POB,∴AE⊥PQ,
因为OB![]() 平面ABCE, AE
平面ABCE, AE![]() 平面ABCE,AE∩OB=O
平面ABCE,AE∩OB=O
∴PQ⊥平面ABCE,∴直线PB与平面ABCE夹角为![]() ,
,
又因为OP=OB,∴OP⊥OB,
∴O、Q两点重合,即OP⊥平面ABCE,
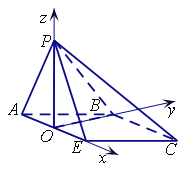
以O为原点,OE为x轴,OB为y轴,OP为z轴,建立空间直角坐标系,由题意得,各点坐标为![]() ,
,
设平面PCE的一个法向量为![]() ,
,
则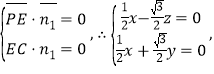
设![]() ,则y=-1,z=1,
,则y=-1,z=1,
∴![]() ,
,
由题意得平面PAE的一个法向量![]() ,
,
设二面角A-EP-C为![]() ,
,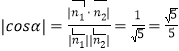 .
.
易知二面角A-EP-C为钝角,所以![]() .
.

 名校课堂系列答案
名校课堂系列答案【题目】某校共有学生2000人,其中男生1100人,女生900人为了调查该校学生每周平均课外阅读时间,采用分层抽样的方法收集该校100名学生每周平均课外阅读时间(单位:小时)
(1)应抽查男生与女生各多少人?
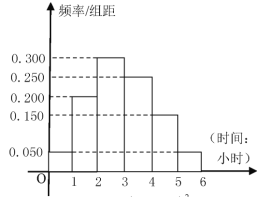
(2)如图,根据收集100人的样本数据,得到学生每周平均课外阅读时间的频率分布直方图,其中样本数据分组区间为![]() .若在样本数据中有38名女学生平均每周课外阅读时间超过2小时,请完成每周平均课外阅读时间与性别的列联表,并判断是否有95%的把握认为“该校学生的每周平均课外阅读时间与性别有关”.
.若在样本数据中有38名女学生平均每周课外阅读时间超过2小时,请完成每周平均课外阅读时间与性别的列联表,并判断是否有95%的把握认为“该校学生的每周平均课外阅读时间与性别有关”.
男生 | 女生 | 总计 | |
每周平均课外阅读时间不超过2小时 | |||
每周平均课外阅读时间超过2小时 | |||
总计 |
附:
| 0.100 | 0.050 | 0.010 | 0.005 |
| 2.706 | 3.841 | 6.635 | 7.879 |
【题目】某企业为了检查生产![]() 产品的甲、乙两条流水线的生产情况,随机地从这两条流水线上生产的大量产品中各抽取50件产品作为样本,测出它们的这一项质量指标值.若该项质量指标值落在
产品的甲、乙两条流水线的生产情况,随机地从这两条流水线上生产的大量产品中各抽取50件产品作为样本,测出它们的这一项质量指标值.若该项质量指标值落在![]() 内,则为合格品,否则为不合格品.下表是甲流水线样本的频数分布表,下图是乙流水线样本的频率分布直方图.
内,则为合格品,否则为不合格品.下表是甲流水线样本的频数分布表,下图是乙流水线样本的频率分布直方图.
甲流水线样本的频数分布表
质量指标值 | 频数 |
| 9 |
| 10 |
| 17 |
| 8 |
| 6 |
乙流水线样本的频率分布直方图
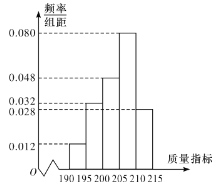
(1)根据图形,估计乙流水线生产的![]() 产品的该项质量指标值的中位数;
产品的该项质量指标值的中位数;
(2)设该企业生产一件合格品获利100元,生产一件不合格品亏损50元,若某个月内甲、乙两条流水线均生产了1000件产品,若将频率视为概率,则该企业本月的利润约为多少元?
【题目】某校在高二年级学生中,对自然科学类、社会科学类校本选修课程的选课意向进行调查.现从高二年级学生中随机抽取180名学生,其中男生105名;在这180名学生中选择社会科学类的男生、女生均为45名.
(1)根据抽取的180名学生的调查结果,完成下面的2×2列联表.
(2)判断能否在犯错误的概率不超过0.025的前提下认为科类的选择与性别有关?
选择自然科学类 | 选择社会科学类 | 合计 | |
男生 | |||
女生 | |||
合计 |
参考公式:![]() ,其中
,其中![]() .
.
P(K2≥k0) | 0.500 | 0.400 | 0.250 | 0.150 | 0.100 | 0.050 | 0.025 | 0.010 | 0.005 | 0.001 | |
k0 | 0.455 | 0.708 | 1.323 | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |