题目内容
9.已知数列{an}满足${a_n}{a_{n+1}}={3^n}$,又a1=1,数列cn=an+an+1,若Sn为{cn}的前n项和,则S2015=2×31008+31003-5.分析 由${a_n}{a_{n+1}}={3^n}$,得${a}_{n+1}{a}_{n+2}={3}^{n+1}$,两式作商得:$\frac{{a}_{n+2}}{{a}_{n}}=3$,由此可得数列{an}的奇数项和偶数项分别构成以3为公比的等比数列,分组后利用等比数列的前n项和求得S2015.
解答 解:由${a_n}{a_{n+1}}={3^n}$,得${a}_{n+1}{a}_{n+2}={3}^{n+1}$,
两式作商得:$\frac{{a}_{n+2}}{{a}_{n}}=3$,
又a1=1,∴a2=3,
则数列{an}的奇数项和偶数项分别构成以3为公比的等比数列,
∴S2015=(a1+a2+…+a2015)+(a2+a3+…+a2016)
=2[(a1+a3+…+a2015)+(a2+a4+…+a2014)]+a2016-a1
=2[$\frac{1×(1-{3}^{1008})}{1-3}+\frac{3×(1-{3}^{1007})}{1-3}$]+31003-1
=2×31008-4+31003-1
=2×31008+31003-5.
故答案为:2×31008+31003-5.
点评 本题考查数列递推式,考查了作商法求数列的通项公式,训练了数列的分组求和,考查等比数列的前n项和,是中档题.

练习册系列答案
相关题目
20.随机观测生产某种零件的某工厂25名工人的日加工零件数(单位:件),获得数据如下:
30,42,41,36,44,40,37,37,25,45,29,43,31,36,49,34,33,43,38,42,32,34,46,39,36.
根据上述数据得到样本的频率分布表如下:
(1)确定样本频率分布表中n1,n2,f1和f2的值;
(2)根据上述频率分布表,画出样本频率分布直方图;
(3)根据样本频率分布直方图,求在该厂任取4人,至少有1人的日加工零件数落在区间(30,35]的概率.
30,42,41,36,44,40,37,37,25,45,29,43,31,36,49,34,33,43,38,42,32,34,46,39,36.
根据上述数据得到样本的频率分布表如下:
| 分组 | 频数 | 频率 |
| [25,30] | 3 | 0.12 |
| (30,35] | 5 | 0.20 |
| (35,40] | 8 | 0.32 |
| (40,45] | n1 | f1 |
| (45,50] | n2 | f2 |
(2)根据上述频率分布表,画出样本频率分布直方图;
(3)根据样本频率分布直方图,求在该厂任取4人,至少有1人的日加工零件数落在区间(30,35]的概率.
14.随机变量X的分布列为
若p1,p2,p3成等差数列,则公差d的取值范围是[-$\frac{1}{3}$,$\frac{1}{3}$].
| X | x1 | x2 | x3 |
| P | p1 | p2 | p3 |
 在四棱锥P-ABCD中(如图),底面ABCD是直角梯形,M为PC中点,且AB∥DC,又∠ABC=45°,DC=1,AB=2,PA⊥平面ABCD,PA=1.
在四棱锥P-ABCD中(如图),底面ABCD是直角梯形,M为PC中点,且AB∥DC,又∠ABC=45°,DC=1,AB=2,PA⊥平面ABCD,PA=1.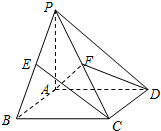 如图,在四棱锥P-ABCD中,底面ABCD是矩形,PA⊥平面ABCD,AP=AB=2,AD=4,E、F依次是PB、PC的中点.
如图,在四棱锥P-ABCD中,底面ABCD是矩形,PA⊥平面ABCD,AP=AB=2,AD=4,E、F依次是PB、PC的中点.