题目内容
18.已知椭圆C:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的离心率为$\frac{1}{2}$,F1、F2分别为椭圆C的左、右焦点,若椭圆C的焦距为2.(1)求椭圆C的方程;
(2)设M为椭圆上任意一点,以M为圆心,MF1为半径作圆M,当圆M与椭圆的右准线l有公共点时,求△MF1F2面积的最大值.
分析 (1)根据焦距为2求出c的值,再由离心率为$\frac{1}{2}$可求出a的值,进而得到b的值,则椭圆方程可求;
(2)先设M的坐标为(x0,y0)根据题意满足$\frac{{x}^{2}}{4}+\frac{{y}^{2}}{3}=1$,再表示出直线l的方程,由圆M与l有公共点可得到M到l的距离4-x0小于或等于圆的半径R,整理可得到关系y02+10x0-15≥0,再由$\frac{{x}^{2}}{4}+\frac{{y}^{2}}{3}=1$消去y0,求出x0的取值范围,写出△MF1F2面积后即可求出最大值.
解答 解:(1)∵2c=2,且$\frac{c}{a}=\frac{1}{2}$,∴c=1,a=2,
∴b2=a2-c2=3.
则椭圆C的方程为$\frac{{x}^{2}}{4}+\frac{{y}^{2}}{3}=1$;
(2)设点M的坐标为(x0,y0),
则$\frac{{{x}_{0}}^{2}}{4}+\frac{{{y}_{0}}^{2}}{3}=1$.
∵F1(-1,0),$\frac{{a}^{2}}{c}=4$,
∴直线l的方程为x=4.
由于圆M与l有公共点,
∴M到l的距离4-x0小于或等于圆的半径R.
∵R2=MF12=(x0+1)2+y02,
∴(4-x0)2≤(x0+1)2+y02,
即y02+10x0-15≥0.
又${{y}_{0}}^{2}=3(1-\frac{{{x}_{0}}^{2}}{4})$,∴3-$\frac{3{{x}_{0}}^{2}}{4}$+10x0-15≥0.
解得:$\frac{4}{3}≤{x}_{0}≤12$,又$\frac{{{x}_{0}}^{2}}{4}+\frac{{{y}_{0}}^{2}}{3}=1$,
∴$\frac{4}{3}≤{x}_{0}<2$,当${x}_{0}=\frac{4}{3}$时,$|{y}_{0}|=\frac{\sqrt{15}}{3}$,
∴$({S}_{△M{F}_{1}{F}_{2}})_{max}=\frac{1}{2}$×2×$\frac{\sqrt{15}}{3}$=$\frac{\sqrt{15}}{3}$.
点评 本题主要考查椭圆的标准方程及其简单性质,考查直线与椭圆、圆与椭圆的交点问题,解答此题的关键在于不等式的转化,属难题.

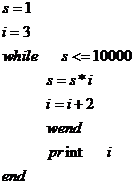
| A. | 求1×2×3×4×…×10 000的值 | |
| B. | 求2×4×6×8×…×10 000的值 | |
| C. | 求3×5×7×9×…×10 000的值 | |
| D. | 求满足1×3×5×…×n>10 000的最小正整数n |
| A. | $\frac{1}{4}$ | B. | $\frac{1}{2}$ | C. | 1 | D. | 2 |
| A. | a<1 | B. | a>1 | C. | a<2 | D. | a>2 |