题目内容
14.随机变量X的分布列为| X | x1 | x2 | x3 |
| P | p1 | p2 | p3 |
分析 根据p1,p2,p3成等差数列,得到p1=$\frac{1}{3}$-d,根据p1 的范围,从而综合求出d的范围.
解答 解:由题意,p2=p1+d,p3=p1+2d.
则p1+p2+p3=3p1+3d=1,
∴p1=$\frac{1}{3}$-d.
又0≤p1≤1,∴0≤$\frac{1}{3}$-d≤1,
即-$\frac{2}{3}$≤d≤$\frac{1}{3}$.
同理,由0≤p3≤1,得-$\frac{1}{3}$≤d≤$\frac{2}{3}$,
∴-$\frac{1}{3}$≤d≤$\frac{1}{3}$.
故答案为:-$\frac{1}{3}$≤d≤$\frac{1}{3}$
点评 本题考察了等差数列的定义,考察了随机变量,由p1=$\frac{1}{3}$-d,根据p1 的范围,求出d的范围是解答问题的关键,本题是一道中档题.

练习册系列答案
相关题目
4.连续抛掷两次骰子得到的点数分别为m和n,记向量$\overrightarrow{a}$=(m,n),向量$\overrightarrow{b}$=(1,-2),则$\overrightarrow{a}$⊥$\overrightarrow{b}$的概率是( )
| A. | $\frac{1}{12}$ | B. | $\frac{1}{6}$ | C. | $\frac{7}{36}$ | D. | $\frac{2}{9}$ |
16.已知等差数列{an}的公差为2,若a1,a3,a4成等比数列,则a2等于( )
| A. | -10 | B. | -8 | C. | -6 | D. | -4 |
 对某班60名学生参加毕业考试成绩(成绩均为整数)整理后,画出频率分布直方图,如图所示,则该班学生及格(60分为及格)人数为( )
对某班60名学生参加毕业考试成绩(成绩均为整数)整理后,画出频率分布直方图,如图所示,则该班学生及格(60分为及格)人数为( )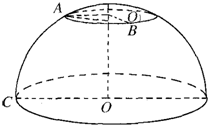 如图,在北纬60°线上,有A、B两地,它们分别在东经20°和140°线上,设地球半径为R,求A、B两地的球面距离.
如图,在北纬60°线上,有A、B两地,它们分别在东经20°和140°线上,设地球半径为R,求A、B两地的球面距离.