题目内容
20.随机观测生产某种零件的某工厂25名工人的日加工零件数(单位:件),获得数据如下:30,42,41,36,44,40,37,37,25,45,29,43,31,36,49,34,33,43,38,42,32,34,46,39,36.
根据上述数据得到样本的频率分布表如下:
| 分组 | 频数 | 频率 |
| [25,30] | 3 | 0.12 |
| (30,35] | 5 | 0.20 |
| (35,40] | 8 | 0.32 |
| (40,45] | n1 | f1 |
| (45,50] | n2 | f2 |
(2)根据上述频率分布表,画出样本频率分布直方图;
(3)根据样本频率分布直方图,求在该厂任取4人,至少有1人的日加工零件数落在区间(30,35]的概率.
分析 (1)利用所给数据,可得样本频率分布表中n1,n2,f1和f2的值;
(2)根据上述频率分布表,可得样本频率分布直方图;
(3)利用对立事件可求概率.
解答 解:(1)(40,45]的频数n1=7,频率f1=0.28;(45,50]的频数n2=2,频率f2=0.08;
(2)频率分布直方图: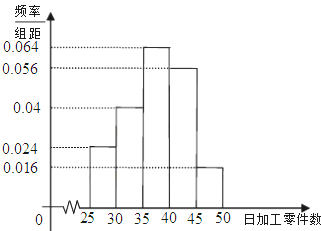
(3)设在该厂任取4人,没有一人的日加工零件数落在区间(30,35]为事件A,则至少有一人的日加工零件数落在区间(30,35]为事件,
已知该厂每人日加工零件数落在区间(30,35]的概率为$\frac{5}{25}$=$\frac{1}{5}$,
∴P(A)=${C}_{4}^{0}(1-\frac{1}{5})^{4}$=0.4096,
∴P($\overline{A}$)=1-P(A)=1-0,4096=0.5904,
∴在该厂任取4人,至少有1人的日加工零件数落在区间(30,35]的概率0.5904.
点评 本题考查了频数分布表,频数分布直方图和概率的计算,属于中档题.

练习册系列答案
相关题目
10.平面区域$\left\{\begin{array}{l}{x+y≥2}\\{x≤1}\\{y≤2}\end{array}\right.$的面积是( )
| A. | $\frac{1}{4}$ | B. | $\frac{1}{2}$ | C. | 1 | D. | 2 |
 对某班60名学生参加毕业考试成绩(成绩均为整数)整理后,画出频率分布直方图,如图所示,则该班学生及格(60分为及格)人数为( )
对某班60名学生参加毕业考试成绩(成绩均为整数)整理后,画出频率分布直方图,如图所示,则该班学生及格(60分为及格)人数为( )