题目内容
17.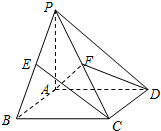 如图,在四棱锥P-ABCD中,底面ABCD是矩形,PA⊥平面ABCD,AP=AB=2,AD=4,E、F依次是PB、PC的中点.
如图,在四棱锥P-ABCD中,底面ABCD是矩形,PA⊥平面ABCD,AP=AB=2,AD=4,E、F依次是PB、PC的中点.(1)求直线EC与平面PAD所成的角(结果用反三角函数值表示);
(2)求三棱锥P-AFD的体积.
分析 (1)解法一:分别以AB、AD、AP为x轴、y轴、z轴建立空间直角坐标系,求出平面PAD的法向量,然后利用向量的数量积求解直线EC与平面PAD所成的角.
解法二:取PA中点G,CD中点H,联结EG、GH、GD说明∠HGD即为直线EC与平面PAD所成的角,然后在Rt△GHD中,求解即可.
(2)解法一:由(1)解法一的建系得,求出平面AFD的法向量,点P到平面AFD的距离为d,
求出底面面积与d,然后求解体积.
解法二:说明PE即为三棱锥P-AFD底面上的高,求出高,求出${S_{△AFD}}=2\sqrt{2}$,即可求解体积.
解法三:利用VP-AFD=VF-PAD=VE-PAD=VD-PAE,转化求解即可.
解答 (1)解法一:分别以AB、AD、AP为x轴、y轴、z轴建立空间直角坐标系,各点坐标分别是A(0,0,0),B(2,0,0),C(2,4,0),D(0,4,0),P(0,0,2),
∴E(1,0,1),F(1,2,1),$\overrightarrow{EC}=(1,4,-1)$,(2分)
又∵AB⊥平面PAD,∴平面PAD的法向量为$\overrightarrow n=\overrightarrow{AB}=(2,0,0)$,(4分)
设直线EC与平面PAD所成的角为α,则$sinα=\frac{{|{\overrightarrow{EC}•\overrightarrow n}|}}{{|\overrightarrow{EC}|•|\overrightarrow n|}}=\frac{2}{{\sqrt{18}•2}}=\frac{{\sqrt{2}}}{6}$,(6分)
∴直线EC与平面PAD所成的角为$arcsin\frac{{\sqrt{2}}}{6}$.(7分)
解法二:∵PA⊥平面ABCD,∴CD⊥PA,又CD⊥AD,∴CD⊥平面PAD,
取PA中点G,CD中点H,联结EG、GH、GD,则EG∥AB∥CD且$EG=\frac{1}{2}AB=1$,∴EGHC是平行四边形,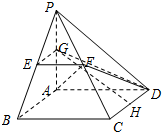
∴∠HGD即为直线EC与平面PAD所成的角.(3分)
在Rt△GAD中,$GD=\sqrt{{1^2}+{4^2}}=\sqrt{17}$,
在Rt△GHD中,$tan∠HGD=\frac{HD}{GD}=\frac{1}{{\sqrt{17}}}=\frac{{\sqrt{17}}}{17}$,(6分)
∴直线EC与平面PAD所成的角为$arctan\frac{{\sqrt{17}}}{17}$.(7分)
(2)解法一:由(1)解法一的建系得,$\overrightarrow{AF}=(1,2,1)$,$\overrightarrow{AD}=(0,4,0)$,
设平面AFD的法向量为$\overrightarrow n=(x,y,z)$,点P到平面AFD的距离为d,
由$\overrightarrow{AF}•\overrightarrow n=0$,$\overrightarrow{AD}•\overrightarrow n=0$得x+2y+z=0且4y=0,
取x=1得$\overrightarrow n=(1,0,-1)$,(9分)
∴$d=\frac{{|{\overrightarrow{AP}•\overrightarrow n}|}}{{|{\overrightarrow n}|}}=\frac{2}{{\sqrt{2}}}=\sqrt{2}$,(11分)
又$|{\overrightarrow{AF}}|=|{\overrightarrow{FD}}|=\sqrt{6}$,∴${S_{△AFD}}=2×\sqrt{6-4}=2\sqrt{2}$,(13分)
∴${V_{P-AFD}}=\frac{1}{3}×2\sqrt{2}×\sqrt{2}=\frac{4}{3}$.(14分)
解法二:易证PE即为三棱锥P-AFD底面上的高,且$|{PE}|=\sqrt{2}$,(11分)
底面△AFD边AD上的高等于AE,且$|{AE}|=\sqrt{2}$,∴${S_{△AFD}}=2\sqrt{2}$(13分)${V_{P-AFD}}=\frac{1}{3}×\frac{1}{2}×4×\sqrt{2}×\sqrt{2}=\frac{4}{3}$.(14分)
解法三:依题意,EF∥平面PAD,∴VP-AFD=VF-PAD=VE-PAD=VD-PAE(11分)${V_{D-PAE}}=\frac{1}{3}×\frac{1}{2}×\frac{1}{2}×|{PA}|×|{AB}|×|{AD}|=\frac{1}{12}×2×2×4=\frac{4}{3}$.(14分)
点评 本题考查几何体的体积的求法,直线与平面所成角的求法,考查空间想象能力以及计算能力.

| A. | a<1 | B. | a>1 | C. | a<2 | D. | a>2 |
 对某班60名学生参加毕业考试成绩(成绩均为整数)整理后,画出频率分布直方图,如图所示,则该班学生及格(60分为及格)人数为( )
对某班60名学生参加毕业考试成绩(成绩均为整数)整理后,画出频率分布直方图,如图所示,则该班学生及格(60分为及格)人数为( )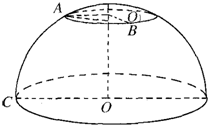 如图,在北纬60°线上,有A、B两地,它们分别在东经20°和140°线上,设地球半径为R,求A、B两地的球面距离.
如图,在北纬60°线上,有A、B两地,它们分别在东经20°和140°线上,设地球半径为R,求A、B两地的球面距离.