题目内容
1．（1）已知（1+ax）5=1+10x+bx2+…+a5x5，则b=40．（2）若（x-2）5=a5x5+a4x4+a3x3+a2x2+a1x+a0，则a1+a2+a3+a4+a5=31．（用数字作答）
分析 （1）由二项式定理，可得（1+ax）5的展开式的通项，写出含x的项，结合题意可得5a=10，即可得a=2，再根据通项可得b=C52a2，计算可得答案；
（2）根据题意，在（x-2）5=a5x5+a4x4+a3x3+a2x2+a1x+a0，令x=0可得a0=-32，令x=1可得a0+a1+a2+a3+a4+a5=-1，两式综合可得答案．
解答 解：（1）（1+ax）5的展开式的通项为Tr+1=C5rarxr，
则含x的项为C51ax=5ax，
又由题意，可得5a=10，即a=2，
则b=C52a2=10×4=40；
（2）在（x-2）5=a5x5+a4x4+a3x3+a2x2+a1x+a0，
令x=0可得，-25=a0，则a0=-32，
令x=1可得，（1-2）5=-1=a0+a1+a2+a3+a4+a5，则a0+a1+a2+a3+a4+a5=-1，
则a1+a2+a3+a4+a5=（a0+a1+a2+a3+a4+a5）-a0=-1+32=31．
故答案为：40，31．
点评 本题考查二项式定理的应用，是给变量赋值的问题，关键是根据要求的结果，选择合适的数值代入，是基础题．
练习册系列答案
相关题目
13．下列程序的功能是（ ）
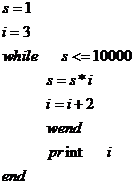
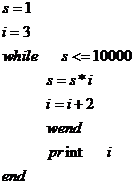
| A． | 求1×2×3×4×…×10 000的值 | |
| B． | 求2×4×6×8×…×10 000的值 | |
| C． | 求3×5×7×9×…×10 000的值 | |
| D． | 求满足1×3×5×…×n＞10 000的最小正整数n |
10．平面区域$\left\{\begin{array}{l}{x+y≥2}\\{x≤1}\\{y≤2}\end{array}\right.$的面积是（ ）
| A． | $\frac{1}{4}$ | B． | $\frac{1}{2}$ | C． | 1 | D． | 2 |
如图，△ABC与△BCD都是边长为2的正三角形，AD=$\sqrt{6}$，PA⊥平面ABC