题目内容
19. 在四棱锥P-ABCD中(如图),底面ABCD是直角梯形,M为PC中点,且AB∥DC,又∠ABC=45°,DC=1,AB=2,PA⊥平面ABCD,PA=1.
在四棱锥P-ABCD中(如图),底面ABCD是直角梯形,M为PC中点,且AB∥DC,又∠ABC=45°,DC=1,AB=2,PA⊥平面ABCD,PA=1.(Ⅰ)求证:CD∥平面MAB;
(Ⅱ)求三棱锥M-PAD的体;
(Ⅲ)若点K线段PA上,试判断平面KBC和平面PAC的位置关系,并加以证明.
分析 (Ⅰ)根据线面平行的判定定理证明即可;(Ⅱ)根据棱锥的体积公式计算即可;(Ⅲ)先求出BC⊥AC,再求出BC⊥平面PAC,从而得到平面PAC⊥平面KBC.
解答 (Ⅰ)证明:因为AB∥CD,
又AB?平面MAB,CD?平面MAB,
∴CD∥平面MAB;
(Ⅱ)解:∵M是PC中点,
∴M到面ADP的距离是C到面ADP距离的一半,
∴${V_{M-ACD}}=\frac{1}{3}{S_{△APD}}•(\frac{1}{2}CD)=\frac{1}{3}×(\frac{1}{2}×1×1)×\frac{1}{2}=\frac{1}{12}$;
(Ⅲ)平面PAC⊥平面KBC,
证明:如图示: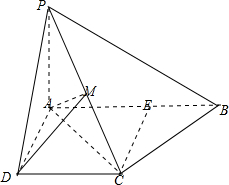
在直角梯形ABCD中,过C作CE⊥AB于点E,
则四边形ADCE为矩形,∴AE=DC=1,又AB=2,∴BE=1,
在Rt△BEC中,∠ABC=45°,
∴$CE=BE=1,CB=\sqrt{2}$,∴AD=CE=1,
则$AC=\sqrt{A{D^2}+C{D^2}}=\sqrt{2}$,AC2+BC2=AB2,
∴BC⊥AC,
又PA⊥平面ABCD,∴PA⊥BC,而PA∩AC=A,
∴BC⊥平面PAC,
又因为BC?平面KBC,所以平面PAC⊥平面KBC.
点评 本题考察了线面平行的判定定理,线面、面面垂直的判定定理,考察棱锥的体积,是一道中档题.

练习册系列答案
相关题目
14.函数 f(x)=(x2-2x)ex的图象大致是( )
| A. | 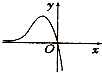 | B. | 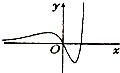 | C. | 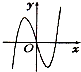 | D. | 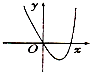 |
4.连续抛掷两次骰子得到的点数分别为m和n,记向量$\overrightarrow{a}$=(m,n),向量$\overrightarrow{b}$=(1,-2),则$\overrightarrow{a}$⊥$\overrightarrow{b}$的概率是( )
| A. | $\frac{1}{12}$ | B. | $\frac{1}{6}$ | C. | $\frac{7}{36}$ | D. | $\frac{2}{9}$ |