题目内容
9．向量|$\overrightarrow{OA}$|=5，|$\overrightarrow{OB}$|=3，＜$\overrightarrow{OA}$，$\overrightarrow{OB}$＞=120°，则$\overrightarrow{OA}$在$\overrightarrow{OB}$上的正射影的数量为$-\frac{5}{2}$．分析 根据射影的定义，便有$\overrightarrow{OA}$在$\overrightarrow{OB}$方向上的射影为|$\overrightarrow{OA}$|cos120°．
解答 解：$|\overrightarrow{OA}|cos＜\overrightarrow{OA}，\overrightarrow{OB}＞$=$5×（-\frac{1}{2}）=-\frac{5}{2}$；
∴$\overrightarrow{OA}$在$\overrightarrow{OB}$上的正射影的数量为$-\frac{5}{2}$．
故答案为：$-\frac{5}{2}$．
点评 考查射影的定义，以及计算射影的公式，$\overrightarrow{a}$在$\overrightarrow{b}$方向上的射影为：$|\overrightarrow{a}|cos＜\overrightarrow{a}，\overrightarrow{b}＞$．
练习册系列答案
相关题目
2．已知△ABC是腰长为2等腰直角三角形，D点是斜边AB的中点，点P在CD上，且$\overrightarrow{CP}=\frac{1}{2}\overrightarrow{PD}$，则$\overrightarrow{PA}•\overrightarrow{PB}$=（ ）
| A． | -$\frac{3}{4}$ | B． | -$\frac{10}{9}$ | C． | 0 | D． | 4 |
4．
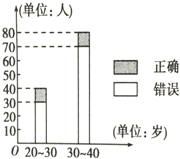“开门大吉”是某电视台推出的游戏节目．选手面对1～8号8扇大门，依次按响门上的门铃，门铃会播放一段音乐（将一首经典流行歌曲以单音色旋律的方式演绎），选手需正确回答出这首歌的名字，方可获得该扇门对应的家庭梦想基金．在一次场外调查中，发现参赛选手多数分为两个年龄段：20～30；30～40（单位：岁），其猜对歌曲名称与否的人数如图所示．
（Ⅰ）写出2×2列联表；判断是否有90%的把握认为猜对歌曲名称是否与年龄有关，说明你的理由；（下面的临界值表供参考）
（Ⅱ）现计划在这次场外调查中按年龄段用分层抽样的方法选取6名选手，并抽取3名幸运选手，求3名幸运选手中至少有一人在20～30岁之间的概率．
（参考公式：K2=$\frac{{n{{（ad-bc）}^2}}}{（a+b）（c+d）（a+c）（b+d）}$其中n=a+b+c+d）
“开门大吉”是某电视台推出的游戏节目．选手面对1～8号8扇大门，依次按响门上的门铃，门铃会播放一段音乐（将一首经典流行歌曲以单音色旋律的方式演绎），选手需正确回答出这首歌的名字，方可获得该扇门对应的家庭梦想基金．在一次场外调查中，发现参赛选手多数分为两个年龄段：20～30；30～40（单位：岁），其猜对歌曲名称与否的人数如图所示．（Ⅰ）写出2×2列联表；判断是否有90%的把握认为猜对歌曲名称是否与年龄有关，说明你的理由；（下面的临界值表供参考）
| P（K2≥k0） | 0.10 | 0.05 | 0.010 | 0.005 |
| k0 | 2.706 | 3.841 | 6.635 | 7.879 |
（参考公式：K2=$\frac{{n{{（ad-bc）}^2}}}{（a+b）（c+d）（a+c）（b+d）}$其中n=a+b+c+d）
14．若向量$\overrightarrow{a}$=（1，2），$\overrightarrow{b}$=（-3，1），则2$\overrightarrow{a}$-$\overrightarrow{b}$=（ ）
| A． | （5，3） | B． | （5，1） | C． | （-1，3） | D． | （-5，-3） |
18．执行如图所示的程序框图，输出的S值为（ ）
| A． | 2 | B． | $\frac{3}{2}$ | C． | $\frac{5}{3}$ | D． | $\frac{8}{5}$ |