题目内容
4.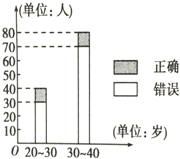 “开门大吉”是某电视台推出的游戏节目.选手面对1~8号8扇大门,依次按响门上的门铃,门铃会播放一段音乐(将一首经典流行歌曲以单音色旋律的方式演绎),选手需正确回答出这首歌的名字,方可获得该扇门对应的家庭梦想基金.在一次场外调查中,发现参赛选手多数分为两个年龄段:20~30;30~40(单位:岁),其猜对歌曲名称与否的人数如图所示.
“开门大吉”是某电视台推出的游戏节目.选手面对1~8号8扇大门,依次按响门上的门铃,门铃会播放一段音乐(将一首经典流行歌曲以单音色旋律的方式演绎),选手需正确回答出这首歌的名字,方可获得该扇门对应的家庭梦想基金.在一次场外调查中,发现参赛选手多数分为两个年龄段:20~30;30~40(单位:岁),其猜对歌曲名称与否的人数如图所示.(Ⅰ)写出2×2列联表;判断是否有90%的把握认为猜对歌曲名称是否与年龄有关,说明你的理由;(下面的临界值表供参考)
| P(K2≥k0) | 0.10 | 0.05 | 0.010 | 0.005 |
| k0 | 2.706 | 3.841 | 6.635 | 7.879 |
(参考公式:K2=$\frac{{n{{(ad-bc)}^2}}}{(a+b)(c+d)(a+c)(b+d)}$其中n=a+b+c+d)
分析 (Ⅰ)利用已知条件直接列出2×2联列表,利用公式求出K,然后判断猜对歌曲名称与否和年龄有关.
(Ⅱ)设事件A为3名幸运选手中至少有一人在20~30岁之间,求出20~30岁,30~40岁的人数,然后求解概率即可.
解答 解:(Ⅰ)
| 年龄/正误 | 正确 | 错误 | 合计 |
| 20~30 | 10 | 30 | 40 |
| 30~40 | 10 | 70 | 80 |
| 合计 | 20 | 100 | 120 |
有90%的把握认为猜对歌曲名称与否和年龄有关.
(Ⅱ)设事件A为3名幸运选手中至少有一人在20~30岁之间,由已知得20~30岁之间的人数为2人,
30~40岁之间的人数为4人,从6人中取3人的结果有20种,
事件A的结果有16种,$P(A)=\frac{16}{20}=\frac{4}{5}$.
点评 本题考查对立检验的应用,古典概型的概率的求法,考查计算能力.

练习册系列答案
 导学与测试系列答案
导学与测试系列答案 新非凡教辅冲刺100分系列答案
新非凡教辅冲刺100分系列答案
相关题目
17.$\frac{1}{2}+({\frac{1}{2}+\frac{1}{4}})+({\frac{1}{2}+\frac{1}{4}+\frac{1}{8}})+…+({\frac{1}{2}+\frac{1}{4}+…+\frac{1}{{{2^{10}}}}})$的值为( )
| A. | 7+$\frac{1}{2^9}$ | B. | 9+$\frac{1}{{{2^{10}}}}$ | C. | 11+$\frac{1}{{{2^{11}}}}$ | D. | 7+$\frac{1}{{{2^{10}}}}$ |
20.若幂函数$y=({{m^2}-5m+7}){x^{{m^2}-6}}$在(0,+∞)单调递增,则实数m值为( )
| A. | 3 | B. | 2 | C. | 2或3 | D. | -2或-3 |
16.通过随机询问200名性别不同的大学生是否爱好“踢毽子运动”,计算得到统计量值k2的观测值k≈4.892,参照下表,得到的正确结论是( )
| P(k2≥k) | 0.10 | 0.05 | 0.010 |
| k | 2.706 | 3.841 | 6.635 |
| A. | 在犯错误的概率不超过5%的前提下,认为“爱好该运动与性别有关” | |
| B. | 在犯错误的概率不超过5%的前提下,认为“爱好该运动与性别无关” | |
| C. | 有99%以上的把握认为“爱好该运动与性有关” | |
| D. | 有99%以上的把握认为“爱好该运动与性别无关” |
13.下列说法正确的是( )
| A. | 已知购买一张彩票中奖的概率为$\frac{1}{1000}$,则购买1000张这种彩票一定能中奖 | |
| B. | 互斥事件一定是对立事件 | |
| C. | 二进制数1101(2)转化为十进制数是13 | |
| D. | 若样本x1,x2…xn的方差为4,则样本x1-1,x2-1,…,xn-1的方差为3 |
