题目内容
2.已知△ABC是腰长为2等腰直角三角形,D点是斜边AB的中点,点P在CD上,且$\overrightarrow{CP}=\frac{1}{2}\overrightarrow{PD}$,则$\overrightarrow{PA}•\overrightarrow{PB}$=( )| A. | -$\frac{3}{4}$ | B. | -$\frac{10}{9}$ | C. | 0 | D. | 4 |
分析 以CB,CA两直线分别为x,y轴,建立坐标系,根据条件可求出C,A,B,D几点的坐标,设P(x,y),而根据$\overrightarrow{CP}=\frac{1}{2}\overrightarrow{PD}$即可求出点P的坐标,从而得出向量$\overrightarrow{PA},\overrightarrow{PB}$的坐标,然后进行数量积的坐标运算即可.
解答 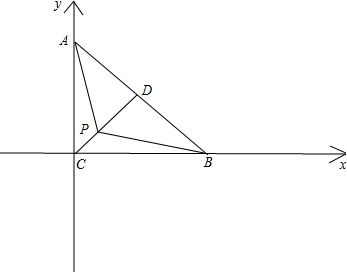 解:如图,分别以边CB,CA所在直线为x,y轴,建立平面直角坐标系,则:
解:如图,分别以边CB,CA所在直线为x,y轴,建立平面直角坐标系,则:
C(0,0),A(0,2),B(2,0),D(1,1);
设P(x,y),∵$\overrightarrow{CP}=\frac{1}{2}\overrightarrow{PD}$;
(x,y)=$\frac{1}{2}$(1-x,1-y);
∴$\left\{\begin{array}{l}{x=\frac{1}{2}(1-x)}\\{y=\frac{1}{2}(1-y)}\end{array}\right.$;
解得$x=y=\frac{1}{3}$;
∴$P(\frac{1}{3},\frac{1}{3})$,$\overrightarrow{PA}=(-\frac{1}{3},\frac{5}{3})$,$\overrightarrow{PB}=(\frac{5}{3},-\frac{1}{3})$;
∴$\overrightarrow{PA}•\overrightarrow{PB}=-\frac{10}{9}$.
故选B.
点评 考查建立平面直角坐标系,利用向量坐标求数量积的方法,由点的坐标可求向量的坐标,向量坐标的数乘、数量积的运算.

练习册系列答案
 优等生题库系列答案
优等生题库系列答案
相关题目
15.已知ξ的分布列如下:
并且η=3ξ+2,则方差Dη=( )
| ξ | 0 | 1 | 2 |
| P | $\frac{1}{2}$ | $\frac{1}{3}$ | $\frac{1}{6}$ |
| A. | $\frac{1}{3}$ | B. | $\frac{2}{3}$ | C. | $\frac{5}{9}$ | D. | 5 |
15.已知函数f(x)=-x3+ax2-x-1在(-∞,+∞)上是单调函数,则实数a的取值范围是( )
| A. | [-$\sqrt{3}$,$\sqrt{3}$] | B. | (-$\sqrt{3}$,$\sqrt{3}$) | C. | (-∞,-$\sqrt{3}$)∪($\sqrt{3}$,+∞) | D. | (-∞,-$\sqrt{3}$)∩($\sqrt{3}$,+∞) |
12.下列给出的赋值语句中正确的是( )
| A. | 4=M | B. | B=A=3 | C. | x+y=0 | D. | M=-M |
7.函数f(x)是周期为4的偶函数,当x∈[0,2]时,f(x)=x-1,则不等式xf(x)>0在[-1,3]上的解集为
( )
( )
| A. | (1,3) | B. | (-1,1) | C. | (-1,0)∪(1,3) | D. | (-1,0)∪(0,1) |
14.甲、乙、丙三地之间有直达的火车,相互之间的距离均不相等,且无通票,问车票票价的种数是( )
| A. | 1 | B. | 2 | C. | 3 | D. | 6 |
10.在西非肆虐的“埃博拉病毒”的传播速度很快,这已经成为全球性的威胁.为了考察某种埃博拉病毒疫苗的效果,现随机抽取100只小鼠进行试验,得到如下列联表:
附表:
参照附表,下列结论正确的是( )
| 感染 | 未感染 | 总计 | |
| 服用 | 10 | 40 | 50 |
| 未服用 | 20 | 30 | 50 |
| 总计 | 30 | 70 | 100 |
| P(K2≥k) | 0.10 | 0.05 | 0.025 |
| k | 2.706 | 3.841 | 5.024 |
| A. | 在犯错误的概率不超5%过的前提下,认为“小动物是否被感染与有没有服用疫苗有关” | |
| B. | 在犯错误的概率不超5%过的前提下,认为“小动物是否被感染与有没有服用疫苗无关” | |
| C. | 有97.5%的把握认为“小动物是否被感染与有没有服用疫苗有关” | |
| D. | 有97.5%的把握认为“小动物是否被感染与有没有服用疫苗无关” |