Question

【题目】已知椭圆C的中心在原点，焦点在x轴上，左、右焦点分别为F1，F2，且|F1F2|=2，点（1， ）在椭圆C上。

（1）求椭圆C的方程；

（2）过F1的直线l与椭圆C相交于A，B两点，且△AF2B的面积为，求以F2为圆心且与直线l相切的圆的方程。

Answer 1

【答案】(1) (2) （x-1）2+y2=2

【解析】试题分析：（1）设椭圆的方程，根据定义求得的值，再根据的关系，求得的值，即可得到椭圆的方程；

(2)当直线轴时，求得，当直线不垂直轴时，设直线的方程为，联立方程组得到和，利用弦长公式求得和点到直线的距离公式求解三角形的高（圆的半径），利用三角形的年级得到，进而得到原的方程.

试题解析：

（1）设椭圆的方程为=1（a>b>0），由题意可得：

椭圆C两焦点坐标分别为F1（-1；0），F2（1，0）.

所以2a=

所以a=2，又c=1，b2=4-1=3，

故椭圆的方程为.

（2）当直线l⊥x轴，计算得到：A（-l，-），B（-1， ），

，不符合题意.

当直线l与x轴不垂直时，设直线l的方程为：y=k（x+1），

由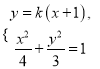消去y得（3+4k2）x2+8k2x+4k2-12=0,

显然△>0成立，设A（x1,y1），B（x2,y2），

则x1+x2=，x1·x2=，

又|AB|=,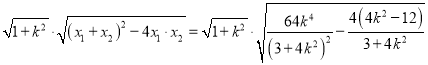

即|AB|=，

又圆F2的半径r=，

所以，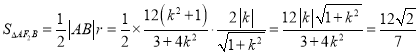

化简，得17k4+k2-18=0，

即（k2-1）（17k2+18）=0，解得k=±1，

所以，r=，故圆F2的方程为：（x-1）2+y2=2.